

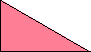
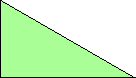
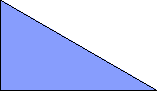
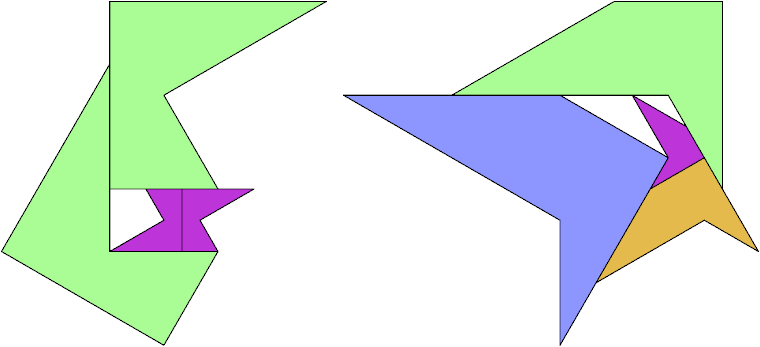
At his website Atlantis, Dr. Karl Scherer introduced similar or scaled tetrads. These are arrangements of four geometrically similar figures in which each borders the other three. That is, they have the same shapes but not the same sizes. In general, scaled tetrads are easier to find that standard tetrads.
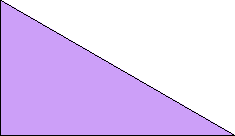
A polydrafter is a polyform whose cells are right triangles with angles 30°, 60°, 90°. It is half an equilateral triangle. Polydrafters whose cells do not conform to the underlying grid of equilateral triangles are called extended polydrafters. For example, there are six proper didrafters and seven more extended didrafters. See Bernd Karl Rennhak's site Logelium for examples.
Here I show the smallest known scaled tetrads for polydrafters with 2 or 3 cells, using a common orientation for the cells, and using scale factors that are integers or integer multiples of √3. If you find a smaller solution or solve an unsolved case, please write.
Bryce Herdt contributed improvements.
See also Scaled Polydom Tetrads.

| 
| 
| 
| 
|
| 1 | √3 | 2 | 3 | 2√3 |
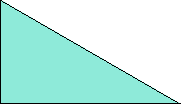
| 
|
| 4 | 3√3 |
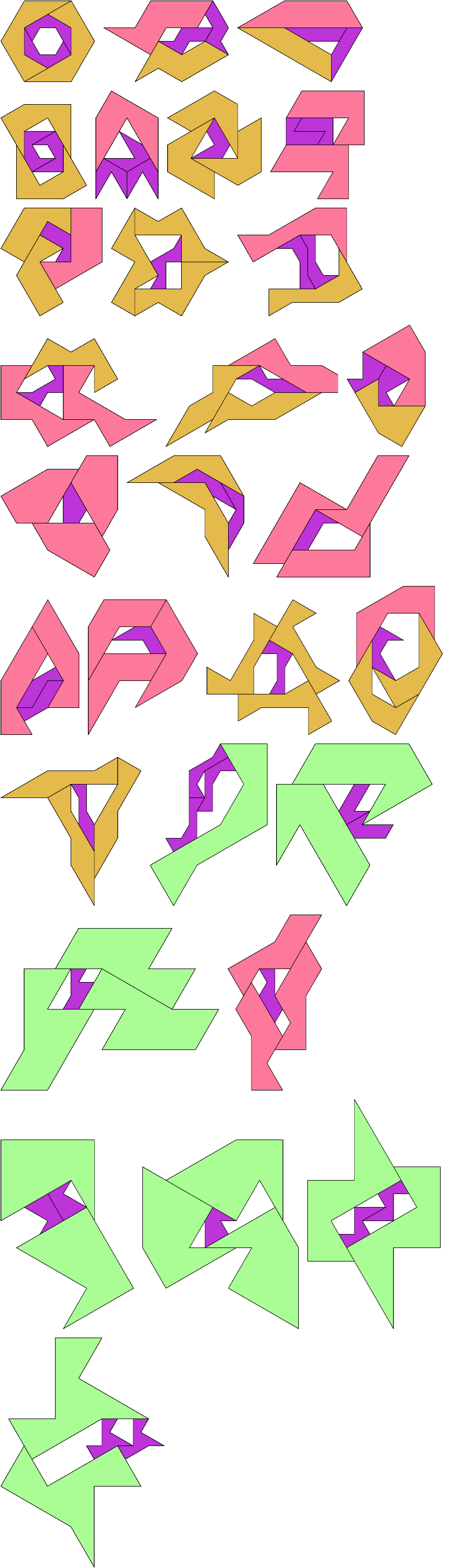
Last revised 2025-12-01.