Issue 23 showed 3-4-5 dissections for pentominoes F, I, L, P, T, V, and Y. Some dissections were found by the editor, Rodolfo Kurchan. The others were found by Mike Reid.
Erich Friedman's Math Magic for December 2009 posed this problem, considering pentominoes and smaller polyominoes as well. He posted dissections by himself, Berend van der Zwaag, Mike Reid, Gavin Theobald, and me. He later posted improved dissections by Livio Zucca and Helmut Postl.
Edo Timmermans has also investigated dissections in which the polyomino at scale 3 is undivided. For want of a prettier term, I call such dissections subglobular.
The first table below shows both unconditional dissections and globular ones. The unconditional dissections are taken from Math Magic.
The second table shows subglobular variants. If you find a solution of either kind with fewer pieces, please write.
For globular 3-4-5 dissections of smaller polyominoes, see Globular 3-4-5 Small Polyomino Dissections.

Because no pieces are rotated, the dissection can be stretched horizontally and vertically to form a rectangle with any dimensions. In particular, it provides a globular dissection of any straight polyomino. If the straight polyomino has 3 or more cells, this globular dissection is minimal.
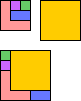
| 5F | 5I | ||||
|---|---|---|---|---|---|
| 
| 
| 
| ||
| GS | 6 | 7 | MR | 4 | 5 |
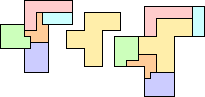
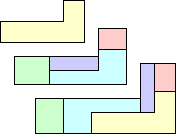
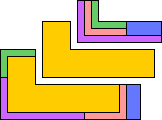
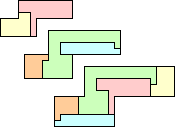
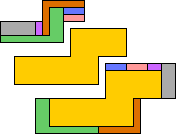
| 5L | 5N | ||||
|---|---|---|---|---|---|
| 
| 
| 
| ||
| BZ | 5 | 5 | GS | 5 | 7 |
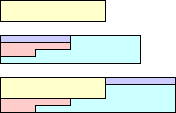
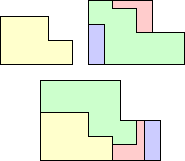
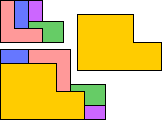
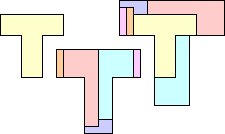
| 5P | 5T | ||||
|---|---|---|---|---|---|
| 
| 
| 
| ||
| LZ | 4 | 5 | GT | 6 | 7 |
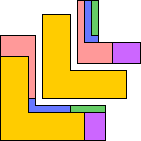
| 5U | 5V | ||||
|---|---|---|---|---|---|
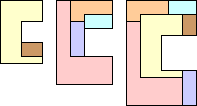
| No solution. | 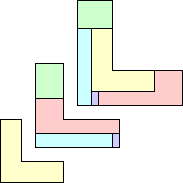
| 
| ||
| GT | 6 | — | MR | 5 | 5 |
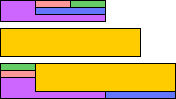
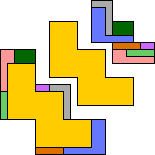
| 5W | 5X | ||||
|---|---|---|---|---|---|

| 
| 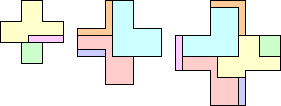
| 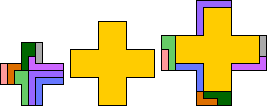
| ||
| GT | 7 | 8 | RR | 7 | 9 |
| 5Y | 5Z | |||||
|---|---|---|---|---|---|---|
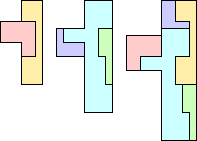
| 
| 
| No solution. | |||
| HP | 5 | ET | 6 | GT | 6 | — |
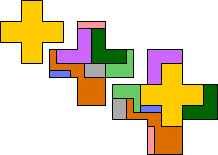
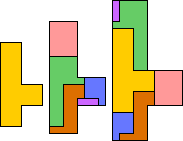
| 5N | 5U | 5W | 5X | 5Y | 5Z | ||
|---|---|---|---|---|---|---|---|
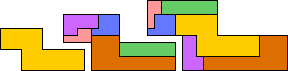
| No solution. | 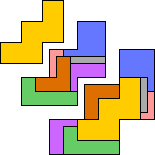
| 
| 
| No solution. | ||
| 6 | — | ET | 7 | ET | 8 | 6 | — |
Last revised 2024-07-17.