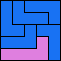Tetromino-Pentomino Oddities
A polyomino oddity
is a symmetrical figure formed by an odd number of copies of
a polyomino.
Symmetrical figures can also be formed with copies of two
different polyominoes.
Since a tetromino has 4 cells and a pentomino has 5,
I use an odd number of cells rather than an odd number of tiles.
Here are the smallest known fully symmetric polyominoes with an odd
number of cells, formed by copies of a given tetromino and pentomino,
using at least one of each.
See also Pentomino Pair Oddities,
Hexiamond Pair Oddities
and Pentahex Pair Oddities.
| 4I+5F 73 | 4I+5I 17 | 4I+5L 25 | 4I+5N 53 | 4I+5P 45 |
|---|
| 
| 
| 
| 
|
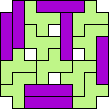
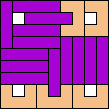
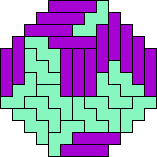
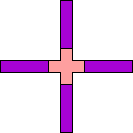
| 4I+5T 89 | 4I+5U 77 | 4I+5V 33 | 4I+5W 129 | 4I+5X 21 |
|---|
| 
| 
| 
| 
|
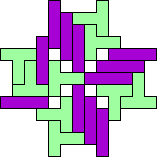
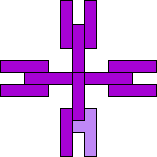
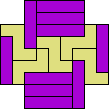
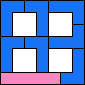
| 4I+5Y 49 | 4I+5Z 65 | 4L+5F 25 | 4L+5I 33 | 4L+5L 25 |
|---|
| 
| 
| 
| 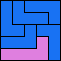
|
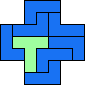
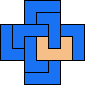
| 4L+5N 25 | 4L+5P 9 | 4L+5T 33 | 4L+5U 33 | 4L+5V 25 |
|---|

| 
| 
| 
| 
|
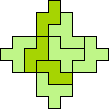
| 4L+5W 41 | 4L+5X 21 | 4L+5Y 17 | 4L+5Z 25 | 4N+5F 37 |
|---|

| 
| 
| 
| 
|
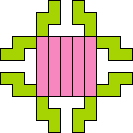
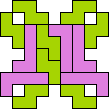
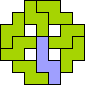
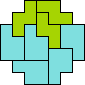
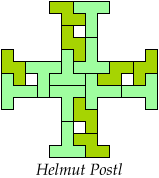
| 4N+5I 57 | 4N+5L 57 | 4N+5N 33 | 4N+5P 37 | 4N+5T 73 |
|---|
| 
| 
| 
| 
|
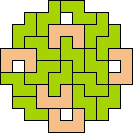
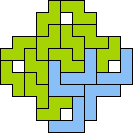
| 4N+5U 85 | 4N+5V 73 | 4N+5W 53 | 4N+5X 21 | 4N+5Y 49 |
|---|
| 
| 
| 
| 
|
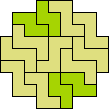
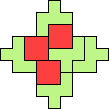
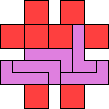
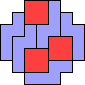
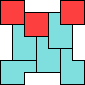
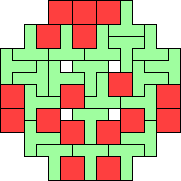
| 4N+5Z 61 | 4Q+5F 37 | 4Q+5I 49 | 4Q+5L 57 | 4Q+5N 37 |
|---|
| 
| 
| 
| 
|
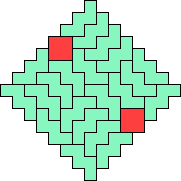
| 4Q+5P 37 | 4Q+5T 173 | 4Q+5U 109 | 4Q+5V 9 | 4Q+5W 113 |
|---|
| 
| 
| 
| 
|
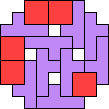
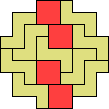
| 4Q+5X 21 | 4Q+5Y 65 | 4Q+5Z 61 | 4T+5F 17 | 4T+5I 13 |
|---|

| 
| 
| 
| 
|
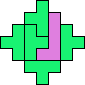
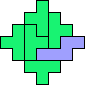
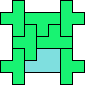
| 4T+5L 25 | 4T+5N 25 | 4T+5P 33 | 4T+5T 17 | 4T+5U 9 |
|---|
| 
| 
| 
| 
|
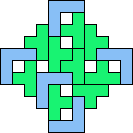
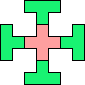
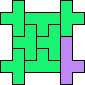
| 4T+5V 61 | 4T+5W 13 | 4T+5X 21 | 4T+5Y 33 | 4T+5Z 45 |
|---|
| 
| 
| 
| 
|
Solutions shown above that are holeless are not shown here.
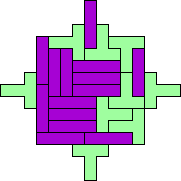
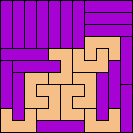
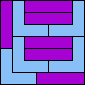
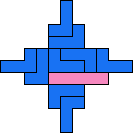
| 4I+5F 77 | 4I+5T 101 | 4I+5U 121 | 4I+5V 49 | 4L+5I 41 |
|---|
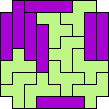
| 
| 
| 
| 
|
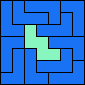
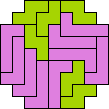
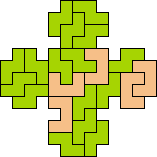
| 4L+5W 49 | 4N+5L 69 | 4N+5N 37 | 4N+5T 77 | 4N+5U 89 |
|---|
| 
| 
| 
| 
|
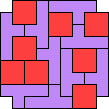
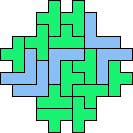
| 4N+5V 77 | 4Q+5T — | 4Q+5U — | 4Q+5Y 77 | 4T+5T 21 |
|---|
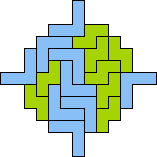
| 
| 
| 
| 
|
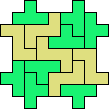
| 4T+5V 73 | 4T+5Z 57 |
|---|
| 
|
Last revised 2020-01-24.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]