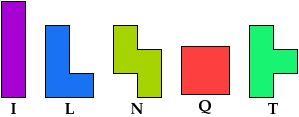

A pentomino is a figure made of 5 squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations.
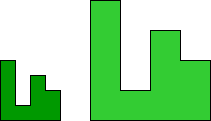
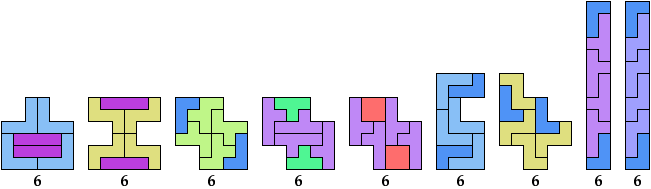
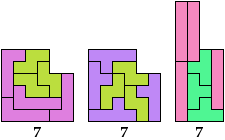
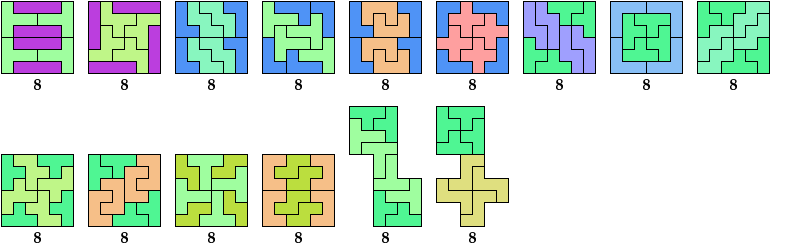
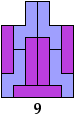
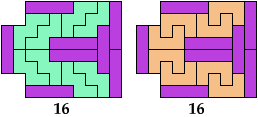
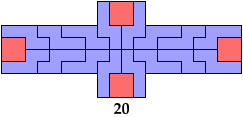
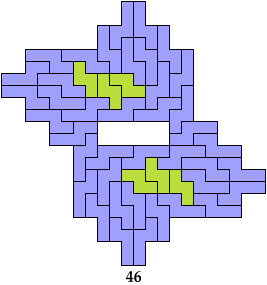
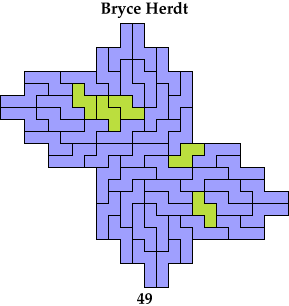
Here I study the problem of arranging copies of a tetromino and a pentomino to form some polyomino that has been scaled up by a factor of 2.
See also
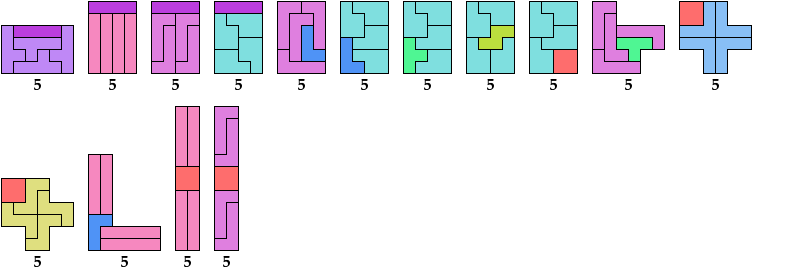
Bryce Herdt solved the pair 4N+5N without holes. My solution with a hole is derived from his solution without one.
Bryce Herdt showed that 4N+5X and 4Q+5X are impossible.
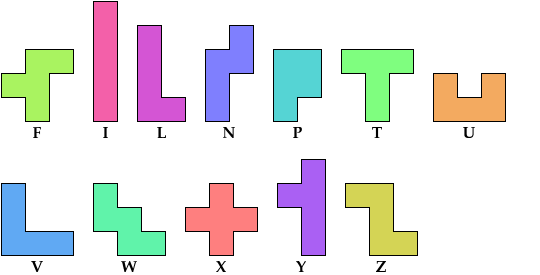
The green indexes are links to tilings by the specified tetromino alone. The blue indexes are links to tilings by the specified pentomino alone.
| F | I | L | N | P | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 36 | 24 | 24 | 40 | 24 | 36 | 72 | 28 | 72 | ? | 24 | 28 |
| L | 28 | 24 | 24 | 28 | 24 | 36 | 36 | 28 | 36 | 36 | 28 | 28 |
| N | ? | 44 | 32 | 224 | 24 | 36 | 36 | 68 | ? | × | 32 | 48 |
| Q | ? | 24 | 24 | 96 | 24 | 64 | ? | 24 | ? | × | 28 | 24 |
| T | 36 | 32 | 24 | 36 | 24 | 36 | 36 | 36 | 36 | 68 | 28 | 36 |
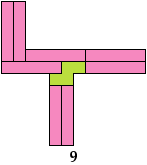
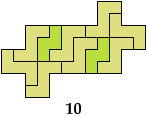
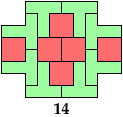
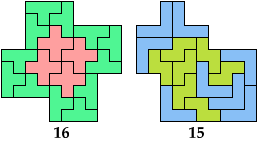
Last revised 2025-10-06.