Pentomino Pairs Tiling a Rectangle with the Four Corner Cells
Removed
A pentomino is a figure made of five squares joined
edge to edge.
There are 12 such figures, not distinguishing reflections and rotations.
They were first enumerated and studied by Solomon Golomb.
The problem of arranging copies of a polyomino to form a rectangle
has been studied for a long time.
Here I study the problem of arranging copies of two pentominoes
to form a rectangle with the four corner cells removed.
Carl Schwenke and Johann Schwenke improved on one of my solutions.
See also
I use Solomon W. Golomb's original names for the pentominoes:
This table shows the smallest total number of copies
of two pentominoes known to be
able to tile a rectangle with three of its corner cells removed,
using at least one copy of each pentomino.
| F | I | L | N | P | T | U | V | W | X | Y | Z |
|---|
| F
| *
| 12
| 10
| 4
| 4
| 41
| 4
| 28
| 4
| ×
| 12
| ×
|
|---|
| I
| 12
| *
| 8
| 9
| 8
| 12
| 52
| 9
| 20
| 4
| 4
| 12
|
|---|
| L
| 10
| 8
| *
| 8
| 4
| 10
| 4
| 10
| 8
| 28
| 8
| 10
|
|---|
| N
| 4
| 9
| 8
| *
| 4
| 9
| 10
| 16
| 10
| 9
| 4
| 12
|
|---|
| P
| 4
| 8
| 4
| 4
| *
| 4
| 8
| 4
| 4
| 9
| 4
| 9
|
|---|
| T
| 41
| 12
| 10
| 9
| 4
| *
| 10
| ×
| 10
| ×
| 20
| ×
|
|---|
| U
| 4
| 52
| 4
| 10
| 8
| 10
| *
| 52
| 8
| 4
| 8
| 72
|
|---|
| V
| 28
| 9
| 10
| 16
| 4
| ×
| 52
| *
| 12
| ×
| 12
| 16
|
|---|
| W
| 4
| 20
| 8
| 10
| 4
| 10
| 8
| 12
| *
| 9
| 8
| 57
|
|---|
| X
| ×
| 4
| 28
| 9
| 9
| ×
| 4
| ×
| 9
| *
| 4
| ×
|
|---|
| Y
| 12
| 4
| 8
| 4
| 4
| 20
| 8
| 12
| 8
| 4
| *
| 12
|
|---|
| Z
| ×
| 12
| 10
| 12
| 9
| ×
| 72
| 16
| 57
| ×
| 12
| *
|
|---|
So far as I know, these solutions
have minimal area. They are not necessarily uniquely minimal.
4 Tiles
8 Tiles
9 Tiles
10 Tiles
12 Tiles
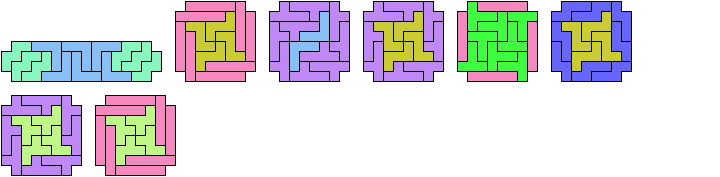
16 Tiles
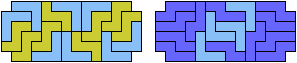
20 Tiles
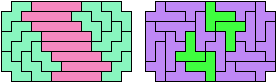
28 Tiles
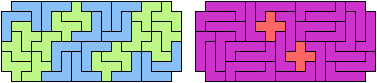
41 Tiles
52 Tiles
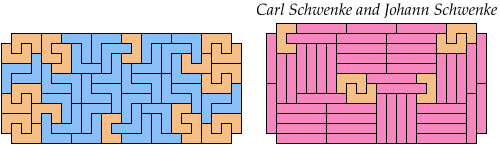
57 Tiles
58 Tiles
72 Tiles
Last revised 2024-02-27.
Back to Polyomino and Polyking Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]