Three-Pentomino Square Frames

Introduction

A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

The January 2008 issue of Erich Friedman's Math Magic defined a frame as a square polyomino with a centered square hole. The problem was to find the frame with least area that could be tiled with a given polyomino.

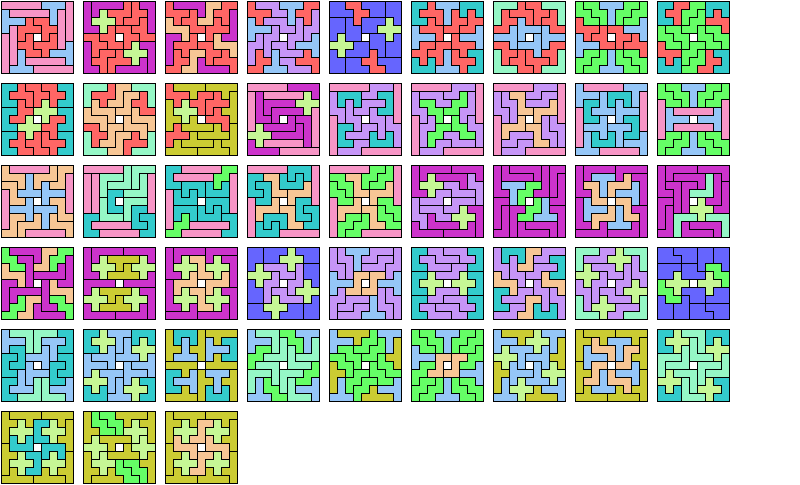
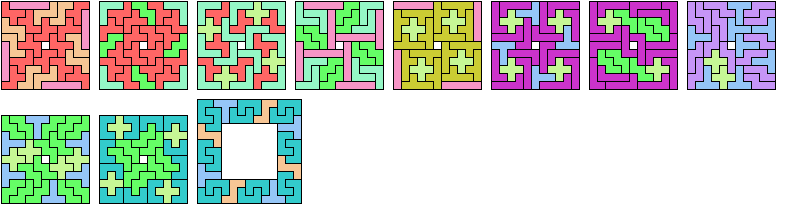
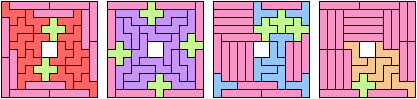
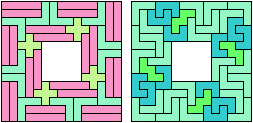
Here I study the related problem of finding the smallest frame that can be tiled with copies of three pentominoes.

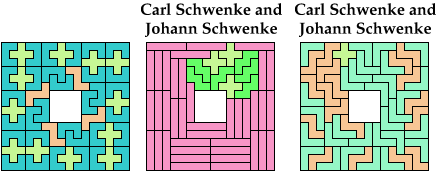
Carl Schwenke and Johann Schwenke improved on two of my solutions.

Nomenclature

I use Solomon W. Golomb's original names for the pentominoes:

Table

F I L	12	F I N	12	F I P	12	F I T	16	F I U	12	F I V	8	F I W	12	F I X	28	F I Y	8	F I Z	24
F L N	8	F L P	12	F L T	12	F L U	12	F L V	12	F L W	12	F L X	16	F L Y	12	F L Z	16	F N P	8
F N T	16	F N U	12	F N V	8	F N W	?	F N X	?	F N Y	12	F N Z	?	F P T	12	F P U	12	F P V	12
F P W	12	F P X	16	F P Y	8	F P Z	12	F T U	16	F T V	16	F T W	16	F T X	?	F T Y	12	F T Z	?
F U V	12	F U W	16	F U X	16	F U Y	12	F U Z	12	F V W	24	F V X	24	F V Y	12	F V Z	16	F W X	?
F W Y	12	F W Z	?	F X Y	16	F X Z	?	F Y Z	12	I L N	8	I L P	8	I L T	12	I L U	12	I L V	8
I L W	12	I L X	16	I L Y	8	I L Z	12	I N P	8	I N T	12	I N U	16	I N V	8	I N W	16	I N X	28
I N Y	8	I N Z	16	I P T	12	I P U	8	I P V	12	I P W	12	I P X	12	I P Y	8	I P Z	12	I T U	16
I T V	12	I T W	16	I T X	28	I T Y	12	I T Z	16	I U V	16	I U W	16	I U X	12	I U Y	12	I U Z	16
I V W	24	I V X	40	I V Y	12	I V Z	12	I W X	48	I W Y	12	I W Z	16	I X Y	24	I X Z	28	I Y Z	12
L N P	8	L N T	12	L N U	12	L N V	8	L N W	12	L N X	16	L N Y	8	L N Z	12	L P T	12	L P U	8
L P V	8	L P W	12	L P X	12	L P Y	12	L P Z	12	L T U	12	L T V	12	L T W	16	L T X	24	L T Y	8
L T Z	16	L U V	12	L U W	12	L U X	12	L U Y	12	L U Z	12	L V W	8	L V X	16	L V Y	8	L V Z	8
L W X	24	L W Y	12	L W Z	16	L X Y	16	L X Z	16	L Y Z	12	N P T	8	N P U	8	N P V	8	N P W	12
N P X	16	N P Y	8	N P Z	12	N T U	12	N T V	12	N T W	12	N T X	24	N T Y	12	N T Z	16	N U V	12
N U W	12	N U X	16	N U Y	12	N U Z	16	N V W	12	N V X	16	N V Y	12	N V Z	12	N W X	?	N W Y	12
N W Z	?	N X Y	12	N X Z	?	N Y Z	12	P T U	12	P T V	12	P T W	12	P T X	12	P T Y	8	P T Z	12
P U V	12	P U W	12	P U X	12	P U Y	8	P U Z	12	P V W	12	P V X	12	P V Y	8	P V Z	8	P W X	16
P W Y	12	P W Z	12	P X Y	12	P X Z	12	P Y Z	12	T U V	16	T U W	12	T U X	16	T U Y	16	T U Z	24
T V W	16	T V X	?	T V Y	12	T V Z	12	T W X	24	T W Y	16	T W Z	16	T X Y	16	T X Z	?	T Y Z	16
U V W	40	U V X	16	U V Y	12	U V Z	12	U W X	24	U W Y	12	U W Z	?	U X Y	16	U X Z	48	U Y Z	12
V W X	56	V W Y	12	V W Z	12	V X Y	12	V X Z	48	V Y Z	12	W X Y	16	W X Z	?	W Y Z	12	X Y Z	16

Basic Solutions

So far as I know, these solutions have minimal area. They are not necessarily uniquely minimal.

8 Tiles

12 Tiles

16 Tiles

24 Tiles

28 Tiles

40 Tiles

48 Tiles

56 Tiles

Separated Solutions

In these solutions, like pentominoes are separated. They may touch at corners. So far as I know, these solutions have minimal area. They are not necessarily uniquely minimal.