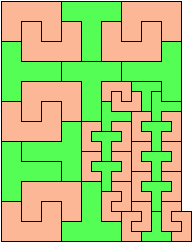
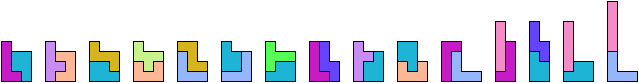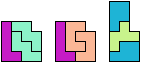Scaled Two-Pentomino L Shapes

  • Introduction
  • Nomenclature
  • Table
  • Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

    Only five scaled pentominoes can tile L-shaped polyominoes:

    Here I show which pairs of pentominoes can tile an L-shaped polyomino, using the pentominoes at various sizes. If you find a solution with fewer tiles than one of mine, please write!

    Bryce Herdt contributed improvements. Carl Schwenke and Johann Schwenke also contributed improvements.

    See also Scaled Two-Pentomino Rectangles.

    Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table

    This table shows the fewest scaled pentominoes known to be able to tile some L-shaped polyomino, using at least one of each pentomino. The L-shaped polyominoes are not necessarily the smallest that can be tiled, only the smallest that can be tiled with the fewest tiles.

    FILNPTUVWXYZ
    F * 6 5 × 3 × 2 4 × × 5 ×
    I 6 * 2 4 2 5 5 2 6 8 4 5
    L 5 2 * 2 2 5 3 2 3 6 5 5
    N × 4 2 * 2 11 6 5 × × 8 ×
    P 3 2 2 2 * 2 2 2 4 6 2 2
    T × 5 5 11 2 * 42 6 15 × 8 ×
    U 2 5 3 6 2 42 * 4 × 6 2 12
    V 4 2 2 5 2 6 4 * 30 × 5 2
    W × 6 3 × 4 15 × 30 * × 8 ×
    X × 8 6 × 6 × 6 × × * 6 ×
    Y 5 4 5 8 2 8 2 5 8 6 * 5
    Z × 5 5 × 2 × 12 2 × × 5 *

    Solutions

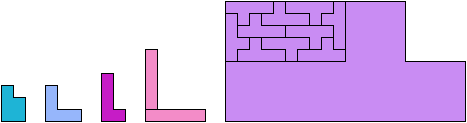
    So far as I know, these solutions have the fewest possible tiles. They are not necessarily uniquely minimal.

    2 Tiles

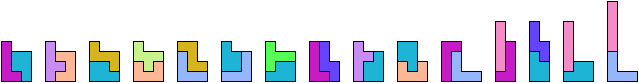
    3 Tiles

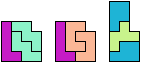
    4 Tiles

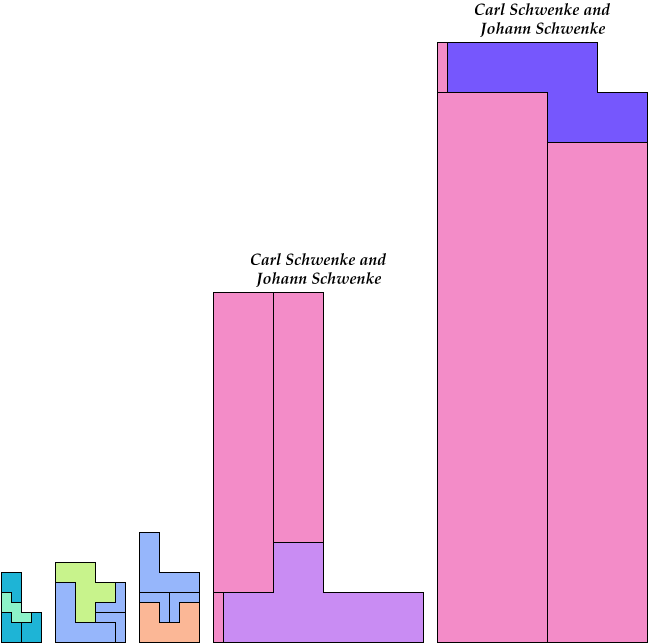
    5 Tiles

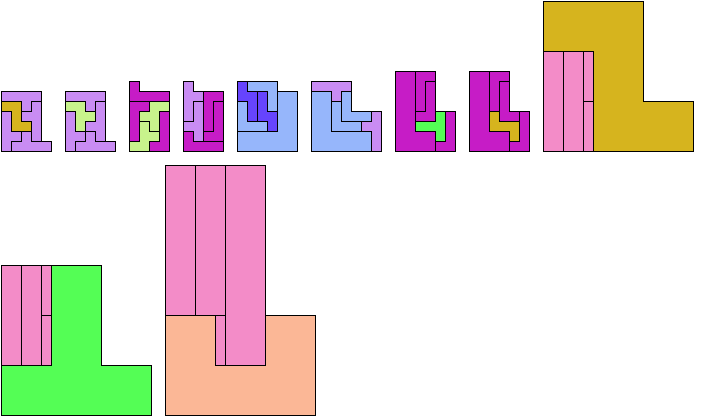
    6 Tiles

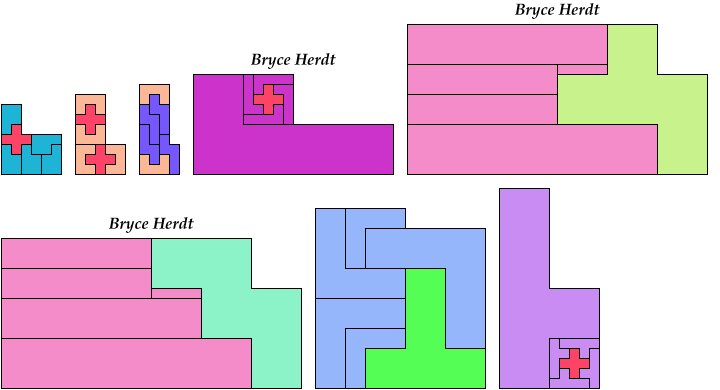
    8 Tiles

    11 Tiles

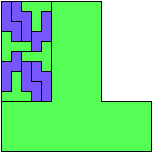
    12 Tiles

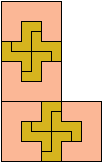
    15 Tiles

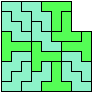
    30 Tiles

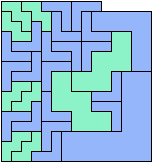
    42 Tiles

    Last revised 2024-02-28.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]