L Shapes from Two Hexominoes

Introduction

If a pair of hexominoes can form a rectangle, they can form an L shape by joining two rectangles, one with each orientation. If the rectangle is a square, three squares can be joined to form an L shape.

Many of the solutions shown were formed in this way, often from rectangular tilings discovered by Mike Reid. They are not all known to be the smallest possible. If you find a smaller solution or solve an unsolved case, please write.

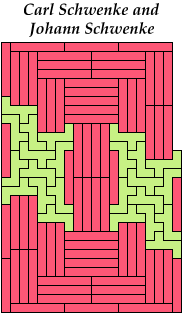
Patrick M. Hamlyn improved some of my solutions. So did Carl Schwenke and Johann Schwenke.

Hexomino Numbers

Table of Results

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
1	•	2	8	8	2	9	2	9	27	12	29	9	3	5	8	3	35	9	29	27	7	27	?	8	5	27	98	29	3	18	2	479	21	?	?
2	2	•	6	2	2	5	2	9	5	7	15	6	3	3	4	3	6	8	16	14	3	10	10	3	12	5	14	10	2	3	2	13	10	13	21
3	8	6	•	19	5	24	6	15	13	19	22	6	6	7	14	2	3	11	16	19	6	8	23	11	8	19	20	41	8	32	3	20	33	188	66
4	8	2	19	•	5	43	5	×	×	34	×	×	6	7	×	4	18	×	×	×	10	31	×	×	14	×	×	×	2	32	4	×	?	×	×
5	2	2	5	5	•	48	2	?	25	54	?	2	3	5	?	3	29	3	6	?	3	6	5	4	6	5	6	2	3	6	2	5	?	?	?
6	9	5	24	43	48	•	2	?	54	300	?	35	13	12	188	36	14	22	28	?	6	204	16	13	?	196	?	?	8	?	5	328	216	?	?
7	2	2	6	5	2	2	•	2	7	2	6	3	3	5	10	3	9	3	5	19	2	5	3	3	8	7	7	5	2	5	2	5	20	7	8
8	9	9	15	×	?	?	2	•	×	800	×	×	36	28	×	28	?	×	×	×	28	?	×	×	?	×	×	×	6	?	3	×	?	×	×
9	27	5	13	×	25	54	7	×	•	37	×	×	19	8	×	8	?	×	×	×	7	?	×	×	?	×	×	×	16	89	10	×	?	×	×
10	12	7	19	34	54	300	2	800	37	•	?	26	10	8	73	12	304	16	?	?	11	75	?	7	?	?	216	?	4	272	3	66	?	?	?
11	29	15	22	×	?	?	6	×	×	?	•	×	6	32	×	20	6	×	×	×	7	28	×	×	?	×	×	×	8	?	8	×	?	×	×
12	9	6	6	×	2	35	3	×	×	26	×	•	15	28	×	16	?	×	×	×	8	?	×	×	?	×	×	×	11	13	5	×	?	×	×
13	3	3	6	6	3	13	3	36	19	10	6	15	•	6	6	4	8	18	14	10	3	6	24	19	10	10	10	13	4	13	3	6	6	3	4
14	5	3	7	7	5	12	5	28	8	8	32	28	6	•	10	3	10	3	8	6	3	23	44	4	19	20	30	15	5	4	5	7	8	7	50
15	8	4	14	×	?	188	10	×	×	73	×	×	6	10	•	4	?	×	×	×	7	16	×	×	6	×	×	×	4	?	8	×	?	×	×
16	3	3	2	4	3	36	3	28	8	12	20	16	4	3	4	•	18	29	8	3	4	36	38	8	10	10	8	10	4	47	3	4	8	36	92
17	35	6	3	18	29	14	9	?	?	304	6	?	8	10	?	18	•	240	200	?	3	?	?	?	?	47	336	?	4	18	10	53	28	?	?
18	9	8	11	×	3	22	3	×	×	16	×	×	18	3	×	29	240	•	×	×	22	?	×	×	?	×	×	×	18	58	7	×	?	×	×
19	29	16	16	×	6	28	5	×	×	?	×	×	14	8	×	8	200	×	•	×	16	?	×	×	?	×	×	×	4	?	10	×	?	×	×
20	27	14	19	×	?	?	19	×	×	?	×	×	10	6	×	3	?	×	×	•	10	?	×	×	?	×	×	×	32	?	?	×	?	×	×
21	7	3	6	10	3	6	2	28	7	11	7	8	3	3	7	4	3	22	16	10	•	8	25	4	25	17	22	22	4	13	4	16	4	34	40
22	27	10	8	31	6	204	5	?	?	75	28	?	6	23	16	36	?	?	?	?	8	•	?	?	?	?	?	?	8	224	10	28	?	?	?
23	?	10	23	×	5	16	3	×	×	?	×	×	24	44	×	38	?	×	×	×	25	?	•	×	?	×	×	×	3	63	9	×	?	×	×
24	8	3	11	×	4	13	3	×	×	7	×	×	19	4	×	8	?	×	×	×	4	?	×	•	32	×	×	×	16	2	4	×	?	×	×
25	5	12	8	14	6	?	8	?	?	?	?	?	10	19	6	10	?	?	?	?	25	?	?	32	•	?	?	?	10	?	6	?	?	?	?
26	27	5	19	×	5	196	7	×	×	?	×	×	10	20	×	10	47	×	×	×	17	?	×	×	?	•	×	×	17	?	10	×	?	×	×
27	98	14	20	×	6	?	7	×	×	216	×	×	10	30	×	8	336	×	×	×	22	?	×	×	?	×	•	×	26	?	14	×	?	×	×
28	29	10	41	×	2	?	5	×	×	?	×	×	13	15	×	10	?	×	×	×	22	?	×	×	?	×	×	•	18	?	6	×	?	×	×
29	3	2	8	2	3	8	2	6	16	4	8	11	4	5	4	4	4	18	4	32	4	8	3	16	10	17	26	18	•	5	3	82	42	5	42
30	18	3	32	32	6	?	5	?	89	272	?	13	13	4	?	47	18	58	?	?	13	224	63	2	?	?	?	?	5	•	9	?	?	?	?
31	2	2	3	4	2	5	2	3	10	3	8	5	3	5	8	3	10	7	10	?	4	10	9	4	6	10	14	6	3	9	•	15	?	57	22
32	479	13	20	×	5	328	5	×	×	66	×	×	6	7	×	4	53	×	×	×	16	28	×	×	?	×	×	×	82	?	15	•	?	×	×
33	21	10	33	?	?	216	20	?	?	?	?	?	6	8	?	8	28	?	?	?	4	?	?	?	?	?	?	?	42	?	?	?	•	?	?
34	?	13	188	×	?	?	7	×	×	?	×	×	3	7	×	36	?	×	×	×	34	?	×	×	?	×	×	×	5	?	57	×	?	•	×
35	?	21	66	×	?	?	8	×	×	?	×	×	4	50	×	92	?	×	×	×	40	?	×	×	?	×	×	×	42	?	22	×	?	×	•
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35

2 Tiles

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

9 Tiles

10 Tiles

11 Tiles

12 Tiles

13 Tiles

14 Tiles

15 Tiles

16 Tiles

17 Tiles

18 Tiles

19 Tiles

20 Tiles

21 Tiles

22 Tiles

23 Tiles

24 Tiles

25 Tiles

26 Tiles

27 Tiles

28 Tiles

29 Tiles

30 Tiles

31 Tiles

32 Tiles

33 Tiles

34 Tiles

35 Tiles

36 Tiles

37 Tiles

38 Tiles

40 Tiles

41 Tiles

42 Tiles

43 Tiles

44 Tiles

47 Tiles

48 Tiles

50 Tiles

53 Tiles

54 Tiles

57 Tiles

58 Tiles

63 Tiles

66 Tiles

73 Tiles

75 Tiles

82 Tiles

89 Tiles

92 Tiles

98 Tiles

188 Tiles

196 Tiles

200 Tiles

204 Tiles

216 Tiles

224 Tiles

240 Tiles

272 Tiles

300 Tiles

304 Tiles

328 Tiles

336 Tiles

479 Tiles

800 Tiles

Last revised 2024-02-28.