Stelo
Stelo
is Jacques Ferroul's set of 12 pieces, which he called the
triapons.
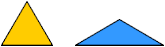
A triapons is formed by joining three cells on the polydrafter grid.
Each cell may be an equilateral
triangle, a moniamond,
or an isosceles triangle with base angles of 30°, a monopons.
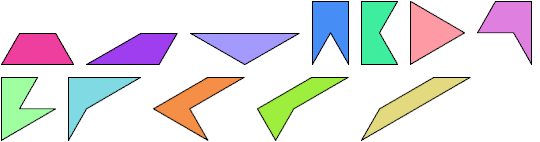
These are the 12 triapons:
Polyiapons may be regarded as a special case of proper polydrafters.
In particular, the triapons are hexadrafters.
Stelo is Esperanto for star.
Ferroul named the set in memory of his grandniece Maïlou.
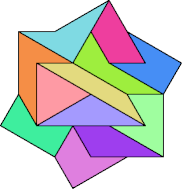
A Lucite set of Stelo is available from Kadon
Enterprises.
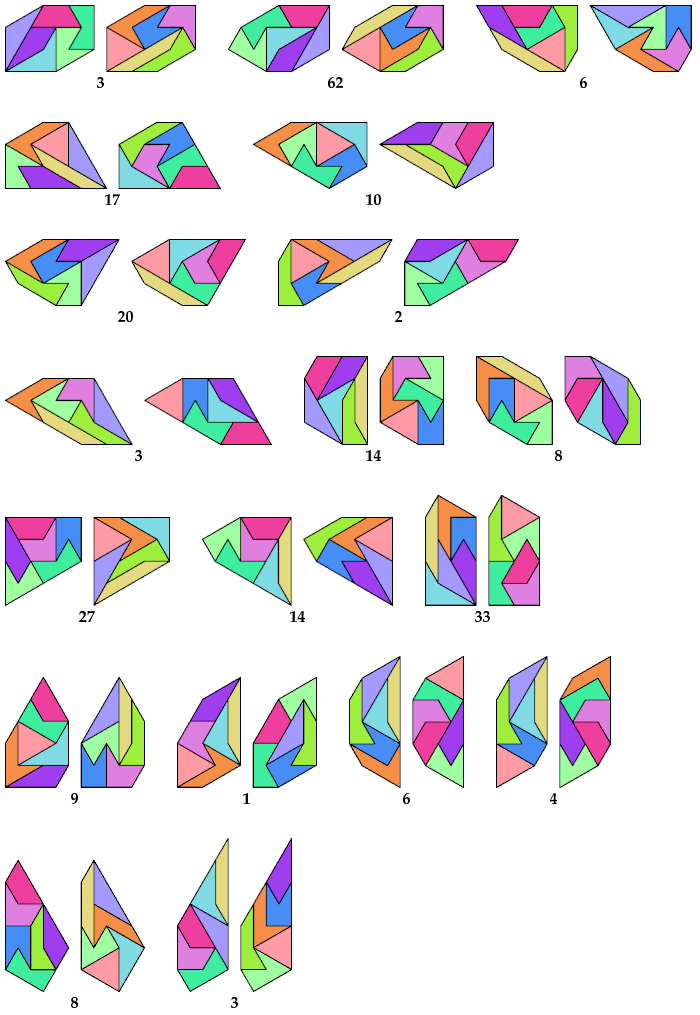
A set of three identical shapes is called triplets.
Stelo can form 17 sets of triplets.
The number below each triplet shows the number of distinct tilings.

A set of two identical shapes is called twins.
Stelo can form 19 sets of convex twins.
The number below each twin shows the number of distinct tilings.
Last revised 2021-02-08.
Back to Polydrafter Tiling
< Polyform Tiling
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]





