Isolated Pentahex Pair Badge Tilings

Introduction

A polyhex is a plane figure formed by joining equal regular hexagons edge to edge. A pentahex is a polyhex with 5 cells. There are 22 pentahexes, not distinguishing reflections and rotations.

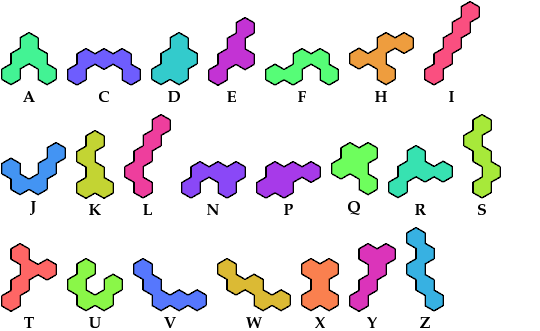
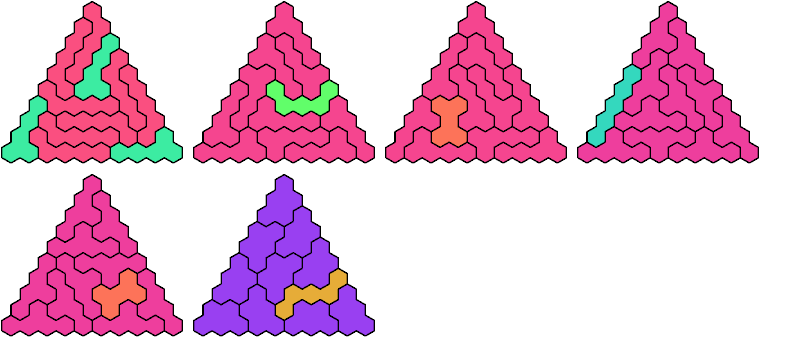
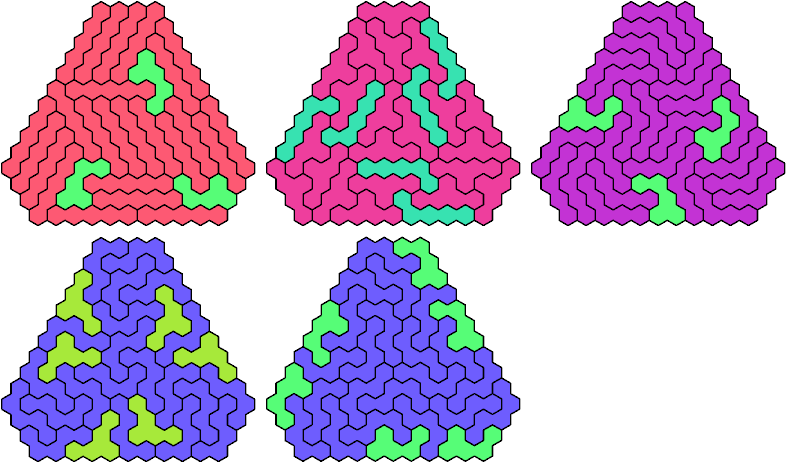
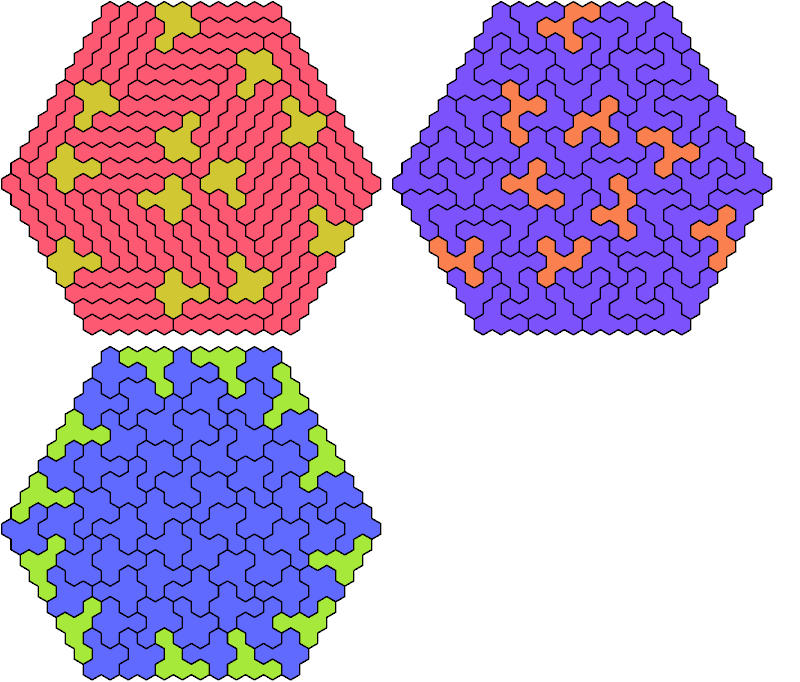
Call a polyhex convex if the region enclosed by joining centers of adjacent cells is convex. A badge is a convex polyhex with 3-rotary symmetry and horizontal mirror symmetry. Here I tile minimal known badges with copies of two pentahexes so that copies of the second pentahex do not touch.

See also

  • Tiling a Badge with Two Pentahexes
  • Isolated Hexomino Pair Rectangles, at Andrew's Blog.

    • Table of Results

    This table shows the number of tiles in the smallest known badges. If you find a smaller badge or solve an unsolved pair, please write.

    Isolated Pentahex
     ACDEFHIJKLNPQRSTUVWXYZ
    A   234 9 2 165 66 9 30 126 24 15 32 18 18 276 213 84 33 ? 18 12 9
    C ?   5 ? ? ? ? ? 18 ? ? 84 ? ? ? ? ? ? 12 ? ? ?
    D 12 5   5 9 12 9 12 9 9 5 5 9 5 11 12 × 9 12 9 2 12
    E 2 93 24   12 63 11 21 29 27 38 9 18 9 87 288 42 93 51 11 33 21
    F 15 ? 15 12   12 15 ? 51 15 27 33 15 27 ? ? ? ? 126 15 54 54
    H ? 12 ? 33 33   60 54 ? 54 33 15 ? 33 ? ? 15 ? ? ? 15 ?
    I 18 123 12 18 126 84   18 84 15 27 15 66 51 126 ? ? 18 ? ? 12 51
    J 54 ? 15 72 ? ? 15   12 75 12 12 75 18 ? 84 ? 15 ? 18 9 75
    K 9 54 9 29 33 ? 24 15   12 33 15 ? 33 ? ? ? 12 ? ? 9 ?
    L 12 12 5 12 12 12 9 12 12   12 12 12 12 12 12 12 12 18 12 11 12
    N 9 15 9 9 15 12 9 9 12 9   15 12 12 15 15 18 15 18 15 9 15
    P 9 12 5 5 5 12 9 12 12 12 9   12 12 12 12 12 12 12 12 9 12
    Q 9 15 21 18 54 ? 33 12 ? 15 18 12   66 ? ? 15 33 ? ? 9 ?
    R 54 33 9 ? 54 ? 33 18 141 32 12 15 ?   ? ? 15 12 ? ? 12 72
    S ? ? 15 ? ? ? ? ? ? ? ? 63 ? ?   ? ? 12 ? ? 9 ?
    T ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?   ? ? ? ? ? ?
    U ? ? ? ? ? ? ? ? 168 ? ? ? ? ? ? ?   15 ? ? 9 ?
    V 51 18 15 29 171 129 15 36 51 18 27 12 29 33 15 29 123   165 60 12 29
    W ? 12 ? 9 ? ? ? ? ? 12 ? 12 ? 51 ? ? ? ?   ? 165 ?
    X 9 ? ? 51 63 ? ? ? ? ? ? 147 ? ? ? ? ? ? ?   ? ?
    Y 9 11 2 15 9 15 9 3 9 9 9 9 12 9 9 15 12 9 12 11   12
    Z 12 18 15 9 60 ? 9 15 ? 12 15 12 ? 15 ? ? 33 15 ? ? 9  

    Navigation

    [2 Tiles] [3 Tiles] [5 Tiles] [9 Tiles] [11 Tiles]
    [12 Tiles] [15 Tiles] [18 Tiles] [21 Tiles] [24 Tiles] [27 Tiles]
    [29 Tiles] [30 Tiles] [32 Tiles] [33 Tiles] [36 Tiles] [38 Tiles]
    [42 Tiles] [51 Tiles] [54 Tiles] [60 Tiles] [63 Tiles] [66 Tiles]
    [72 Tiles] [75 Tiles] [84 Tiles] [87 Tiles] [93 Tiles] [123 Tiles]
    [126 Tiles] [129 Tiles] [141 Tiles] [147 Tiles] [165 Tiles] [168 Tiles]
    [171 Tiles] [213 Tiles] [234 Tiles] [276 Tiles] [288 Tiles]

    2 Tiles

    3 Tiles

    5 Tiles

    9 Tiles

    11 Tiles

    12 Tiles

    15 Tiles

    18 Tiles

    21 Tiles

    24 Tiles

    27 Tiles

    29 Tiles

    30 Tiles

    32 Tiles

    33 Tiles

    36 Tiles

    38 Tiles

    42 Tiles

    51 Tiles

    54 Tiles

    60 Tiles

    63 Tiles

    66 Tiles

    72 Tiles

    75 Tiles

    84 Tiles

    87 Tiles

    93 Tiles

    123 Tiles

    126 Tiles

    129 Tiles

    141 Tiles

    147 Tiles

    165 Tiles

    168 Tiles

    171 Tiles

    213 Tiles

    234 Tiles

    276 Tiles

    288 Tiles

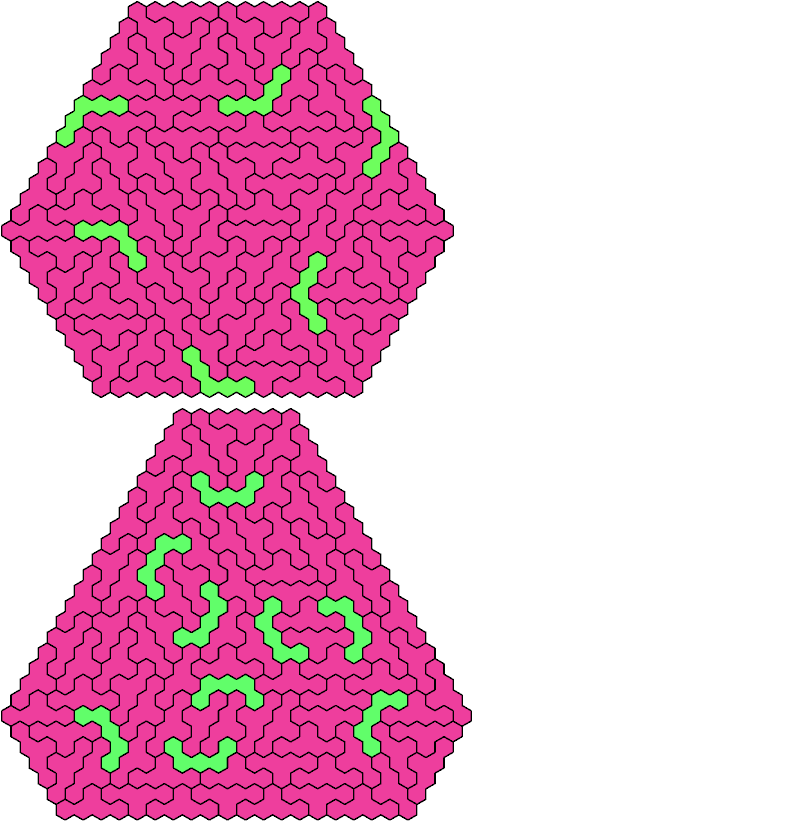
    Last revised 2025-06-18.

    Back to Polyhex Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]