Diabolo-Pentabolo Pair Oddities
A polyabolo oddity
is a symmetrical figure formed by an odd number of copies of
a polyabolo.
Symmetrical figures can also be formed with copies of two
different polyaboloes.
Here are the smallest known fully symmetric polyaboloes with an odd
number of tiles, formed by copies of a given diabolo and pentabolo,
using at least one of each.
See also
Diabolo-Triabolo Pair Oddities,
Triabolo-Tetrabolo Pair Oddities,
Pentomino Pair Oddities,
Hexiamond Pair Oddities,
Trikite-Tetrakite Pair Oddities,
and Pentahex Pair Oddities.
Johann Schwenke contributed improvements.
3 Tiles

5 Tiles

7 Tiles

9 Tiles
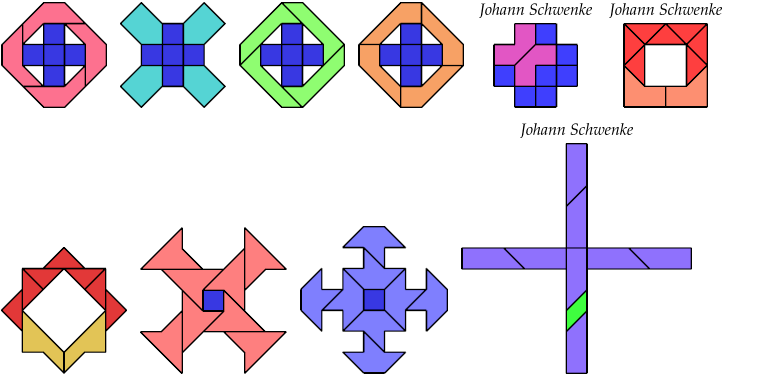
11 Tiles

13 Tiles

15 Tiles
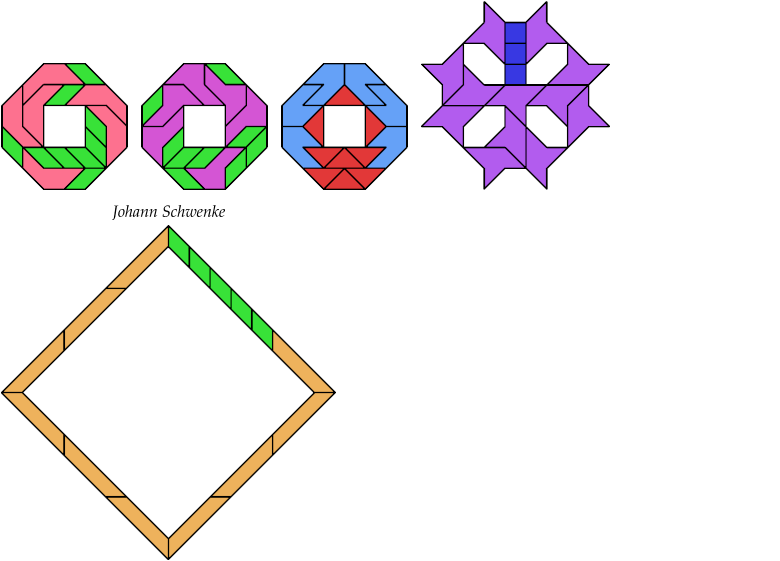
17 Tiles
19 Tiles

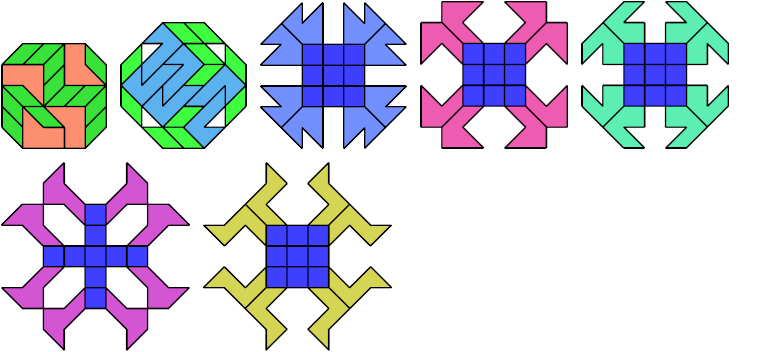
21 Tiles
23 Tiles

25 Tiles
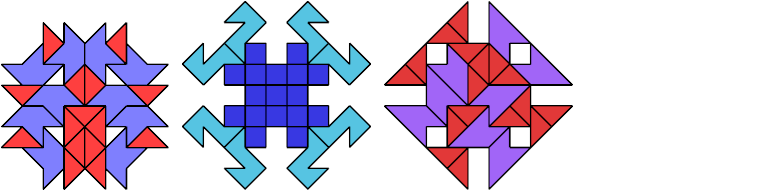
27 Tiles

29 Tiles

31 Tiles
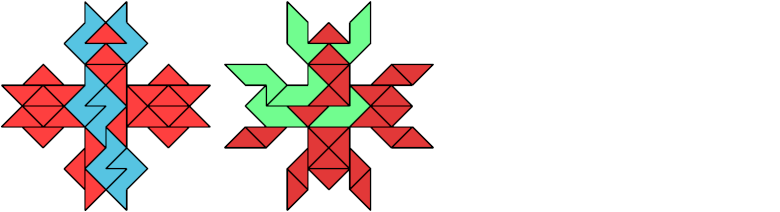
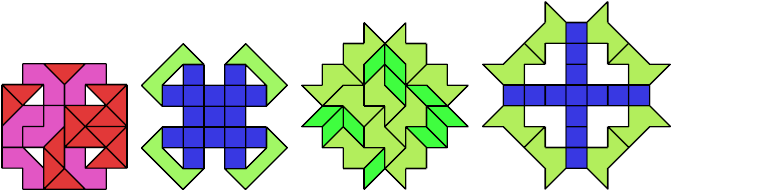
33 Tiles

41 Tiles

Unsolved Pair

Last revised 2022-09-21.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]

















