Triabolo-Tetrabolo Pair Oddities

Introduction

A polyabolo oddity is a symmetrical figure formed by an odd number of copies of a polyabolo. Symmetrical figures can also be formed with copies of two different polyaboloes.

Here are the smallest known fully symmetric polyaboloes with an odd number of tiles, formed by copies of a given triabolo and tetrabolo, using at least one of each.

See also Diabolo-Triabolo Pair Oddities, Diabolo-Pentabolo Pair Oddities, Pentomino Pair Oddities, Hexiamond Pair Oddities, Pentahex Pair Oddities, and Trikite-Tetrakite Pair Oddities,

Solutions

Helmut Postl and Johann Schwenke found some new and improved solutions.

5 Tiles

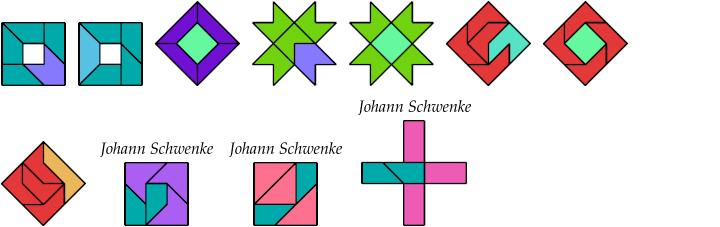
7 Tiles

9 Tiles

11 Tiles

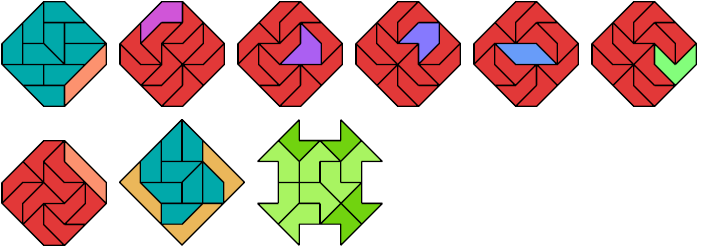
13 Tiles

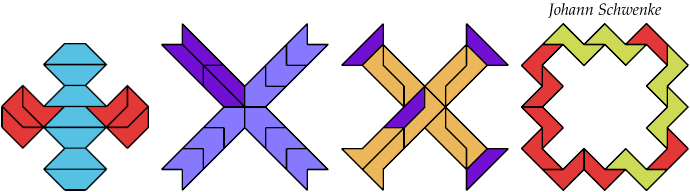
15 Tiles

17 Tiles

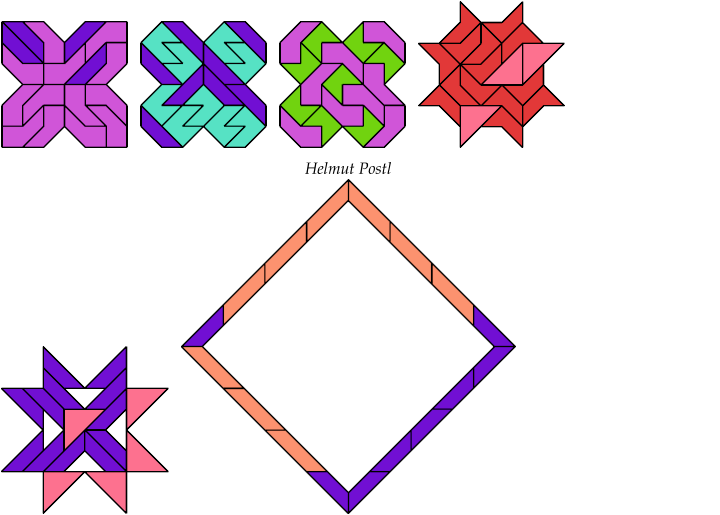
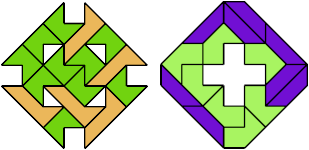
19 Tiles

21 Tiles

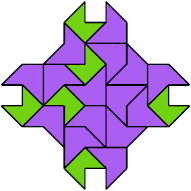
25 Tiles

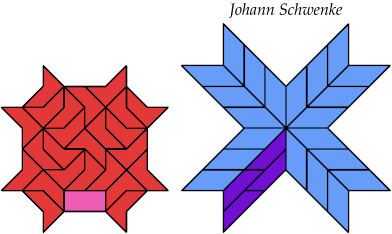
43 Tiles

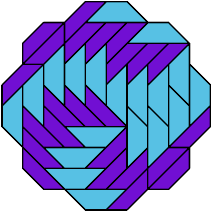
49 Tiles

Unsolved Pairs

Last revised 2022-09-22.

Back to Polyform Oddities < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]