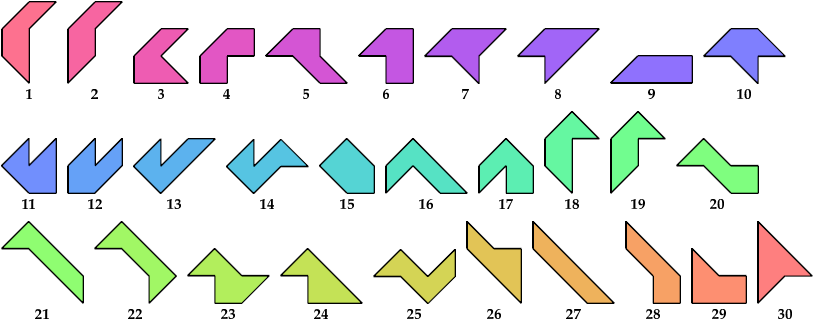

A scaled pentabolo is a pentabolo whose size may be altered without changing its shape. In geometric terms, it is a family of similar pentaboloes.
A trapezium (trapezoid in Canada and the U.S.) is a plane figure with four sides, two of them parallel. A right trapezium is a trapezium with one side perpendicular to the parallel sides.
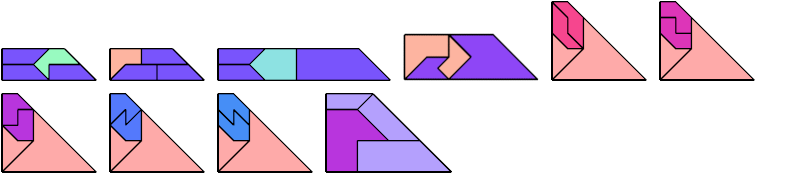
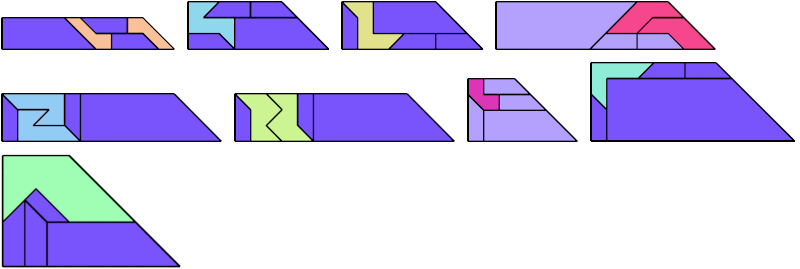
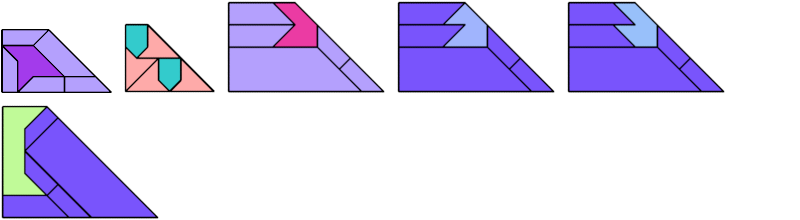
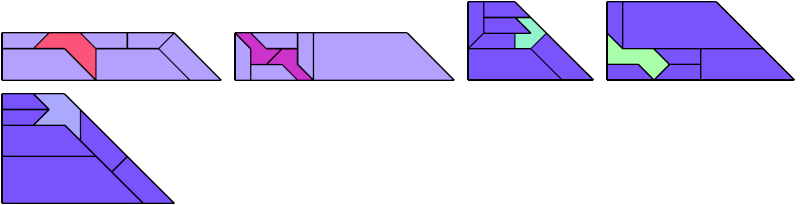
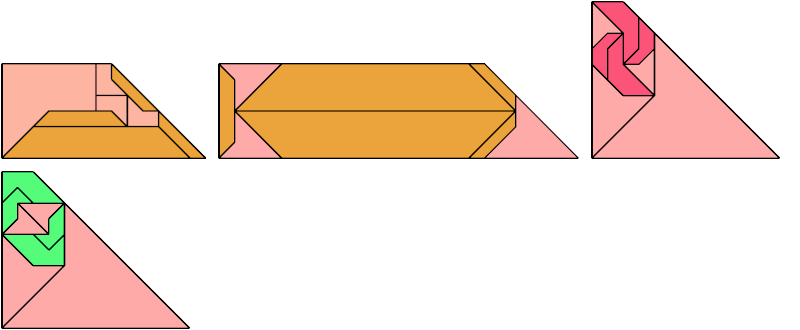
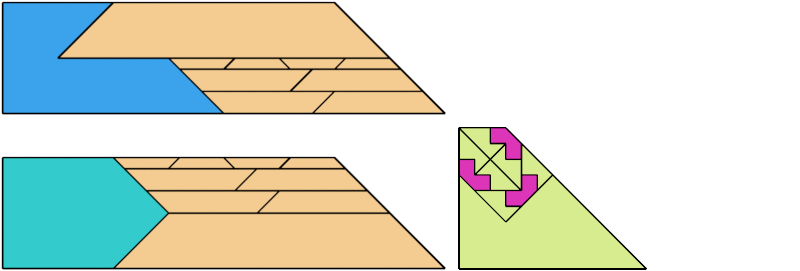
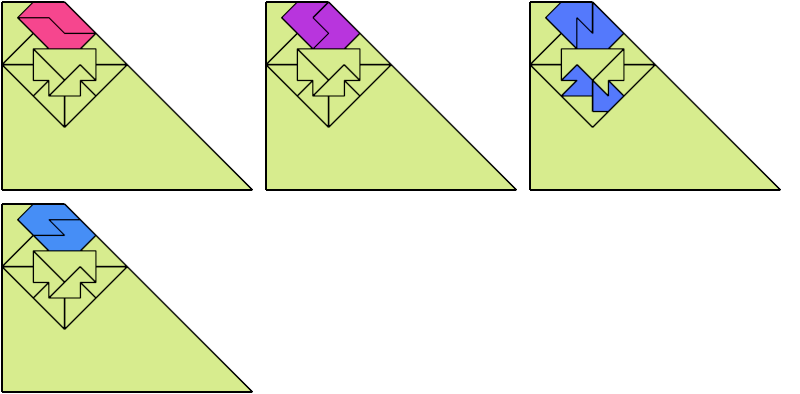
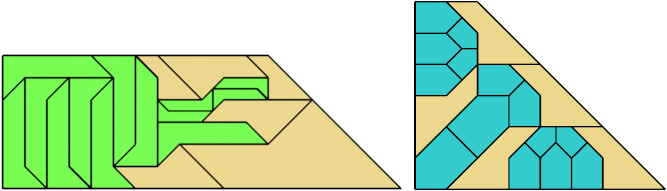
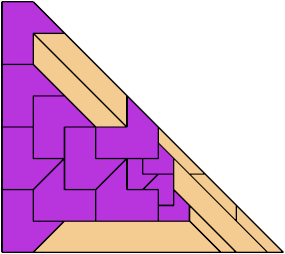
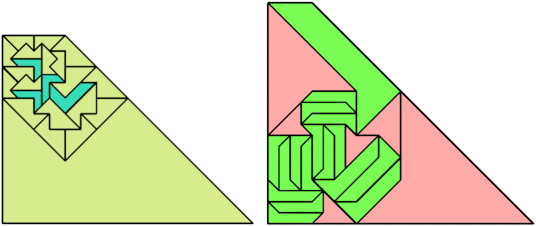
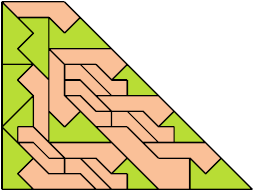
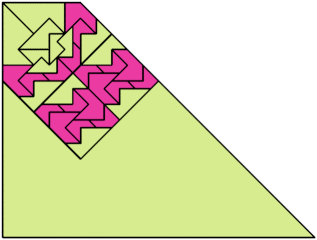
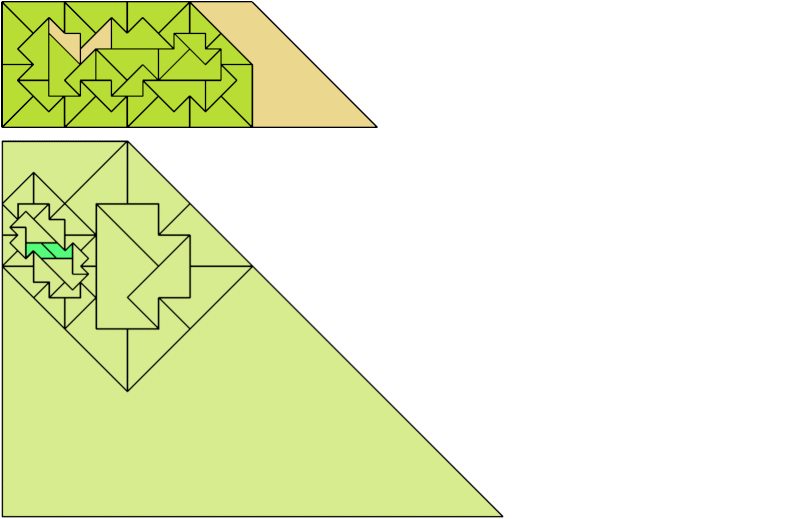
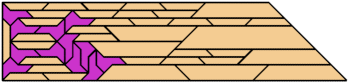
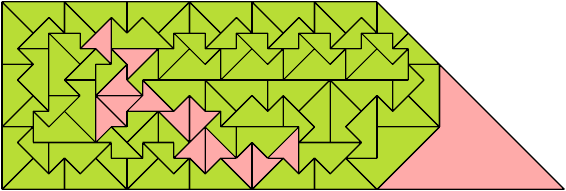
For every pair of scaled pentaboloes, I show a trapezium that they can tile, using at least one of each, and using as few tiles as known to be possible. If you find a smaller solution or solve an unsolved case, please write.
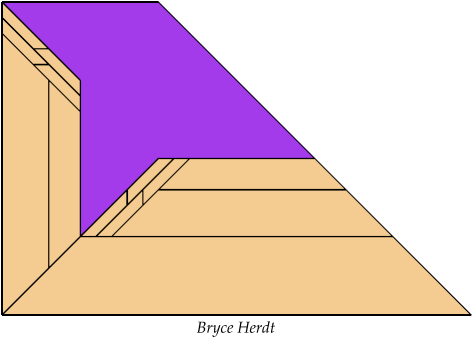
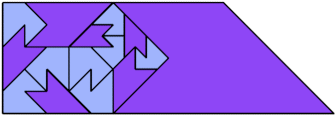
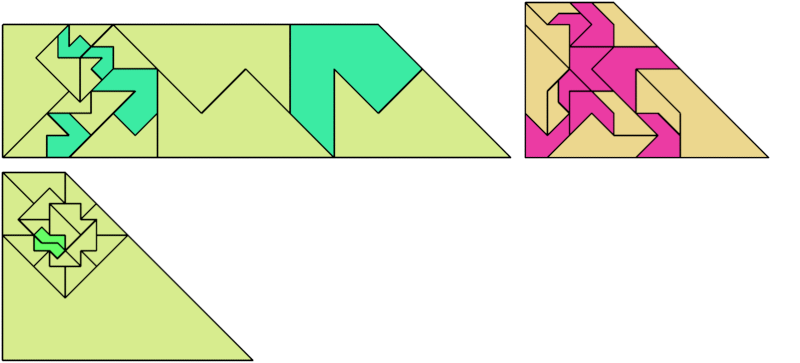
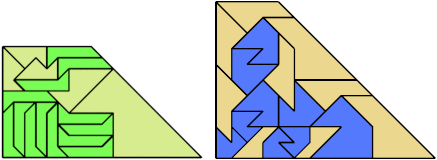
Bryce Herdt found new and improved solutions.
See also
Theoretically, scaled pentabolo 24 and any other scaled pentabolo can together tile a trapezium. I do not have tilings for all such pairs of scaled pentaboloes.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | ? | • | ? | ? | ? | ? | ? | ? | 5 | ? | ? | ? | 2 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | 13 | ? | ? | ? | ? | ? | 4 |
| 8 | ? | ? | ? | ? | ? | ? | ? | • | 3 | ? | 15 | ? | ? | ? | 2 | ? | ? | ? | ? | ? | 22 | ? | ? | 33 | ? | ? | ? | ? | 4 | ? |
| 9 | 7 | 5 | 6 | 5 | 7 | 4 | 6 | 3 | • | 7 | 6 | 6 | 5 | 5 | 4 | 5 | 7 | 4 | 5 | 7 | 3 | 6 | 5 | 3 | 5 | 3 | 2 | 5 | 4 | 2 |
| 24 | ? | 13 | 32 | 10 | ? | 13 | ? | 33 | 3 | ? | 13 | 13 | ? | ? | 2 | 23 | 17 | ? | 33 | 17 | 18 | 27 | ? | • | ? | 33 | 12 | 30 | 10 | 89 |
| 26 | ? | ? | 17 | ? | ? | 3 | ? | ? | 3 | ? | 18 | ? | 2 | ? | 19 | ? | ? | ? | ? | ? | 19 | ? | ? | 33 | ? | • | ? | ? | ? | ? |
| 27 | ? | ? | ? | ? | 49 | 21 | 14 | ? | 2 | ? | 22 | ? | 10 | ? | 10 | ? | ? | ? | ? | ? | 2 | ? | ? | 12 | ? | ? | • | ? | 8 | 8 |
| 30 | 8 | 4 | 27 | 4 | ? | 4 | ? | ? | 2 | ? | 4 | 4 | ? | ? | 6 | 22 | ? | ? | 8 | ? | 23 | ? | ? | 89 | ? | ? | 8 | ? | ? | • |





Last revised 2025-10-18.