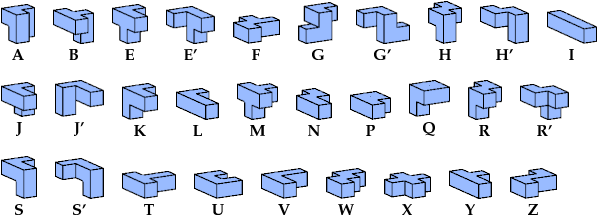

A cubic polycube is a polycube whose cells form the shape of a cube.
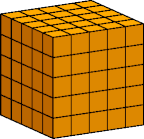
A cube with side n has n3 cells. The smallest cubic polycube whose volume is a multiple of 5 is the cube with side 5, shown above. It has 125 cells, so it can be tiled with 25 pentacubes.
Here I show which pairs of pentacubes can tile the a 5×5×5 cube, using at least one copy of each pentacube. A prime mark (′) after a letter denotes a mirror image. For example, S′ is the mirror image of S. To see a tiling, click on the corresponding entry in the table below. Missing entries indicate unsolved cases. Yellow cells indicate that the tiling is unique.
The E (and E′), I, J (and J′), L, N, P, and Y pentacubes can each tile the 5×5×5 cube alone. To see such tilings, click on the corresponding index link in the table.
If you solve an unsolved case, please write.
See also Tiling a Cuboctal Polycube with Two Pentacubes, Tiling a Rhonic Polycube with Two Pentacubes, and Pentacube Pair Pyramids.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | @ | @ | @ | × | – | @ | @ | @ | @ | @ | @ | @ | – | – | @ | @ | @ | @ | @ | × | @ | @ | |||||||
| B | @ | @ | × | @ | @ | @ | @ | @ | × | @ | @ | @ | @ | @ | @ | @ | @ | @ | × | @ | @ | ||||||||
| E | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | |||
| F | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | × | @ | @ | ||||||||||
| G | × | × | × | × | @ | @ | @ | @ | × | @ | @ | – | × | × | × | @ | × | @ | @ | × | × | @ | × | ||||||
| H | × | @ | @ | @ | @ | @ | @ | @ | @ | – | – | – | @ | @ | @ | @ | @ | @ | × | @ | @ | ||||||||
| I | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | |||||||||||||
| J | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | |||||||||||
| K | @ | @ | @ | @ | @ | @ | – | @ | @ | @ | @ | @ | @ | @ | |||||||||||||||
| L | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | ||||||||||||||||
| M | @ | @ | @ | × | @ | @ | @ | × | @ | × | @ | × | |||||||||||||||||
| N | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | ||||||||||||||||||
| P | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | |||||||||||||||||||
| Q | – | @ | @ | @ | @ | @ | @ | @ | @ | ||||||||||||||||||||
| R | × | @ | @ | @ | @ | @ | @ | × | @ | @ | |||||||||||||||||||
| S | × | @ | @ | @ | @ | × | @ | @ | |||||||||||||||||||||
| T | @ | @ | × | × | @ | @ | |||||||||||||||||||||||
| U | @ | @ | @ | @ | @ | ||||||||||||||||||||||||
| V | @ | × | @ | @ | |||||||||||||||||||||||||
| W | × | @ | × | ||||||||||||||||||||||||||
| X | @ | × | |||||||||||||||||||||||||||
| Y | @ | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||
Last revised 2025-07-28.