Scaled Pentomino Triples Tiling a Rectangle with the Four Corner Cells Removed

  • Introduction
  • Nomenclature
  • Table
  • Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

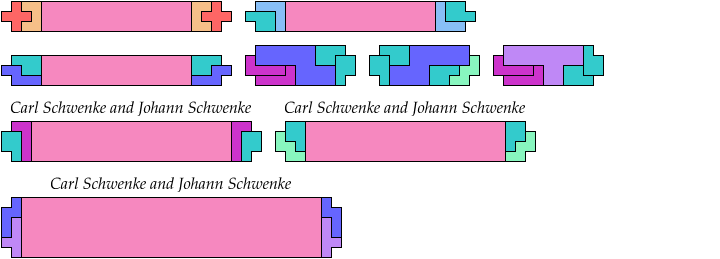
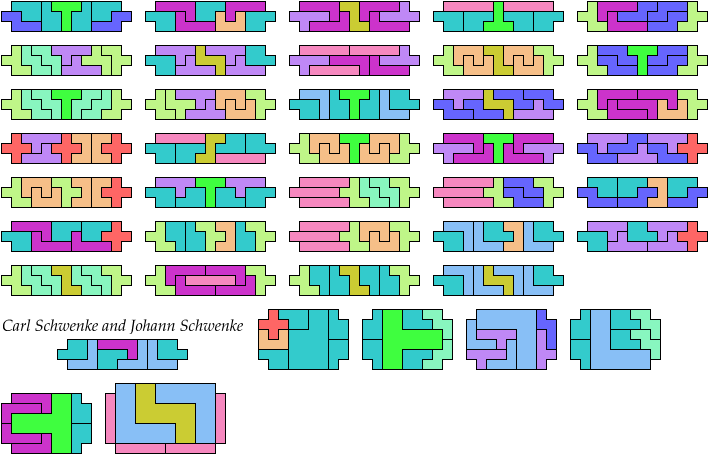
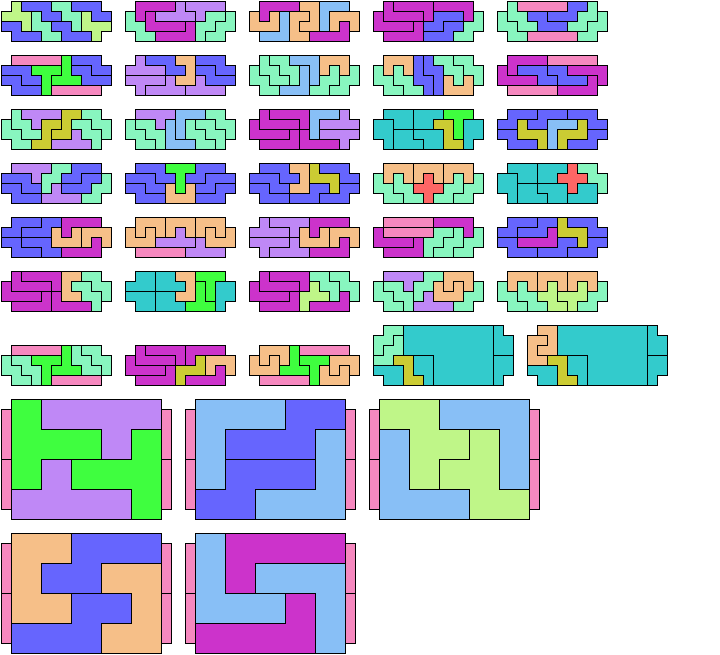
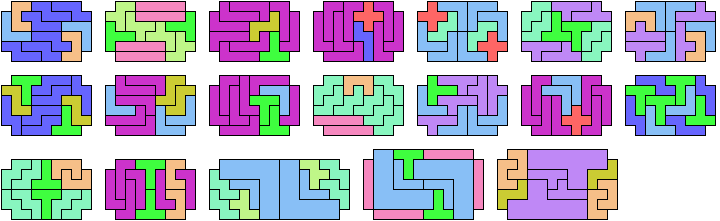
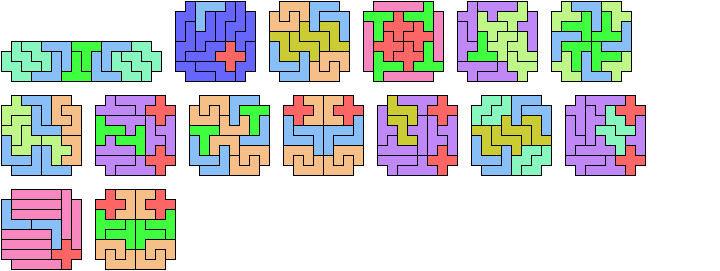
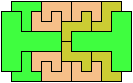
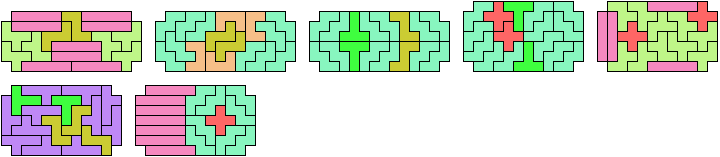
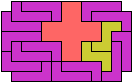
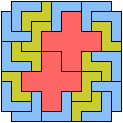
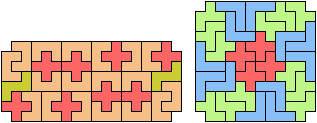
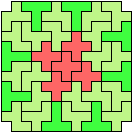
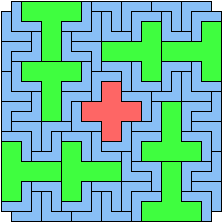
    Here I study the problem of arranging copies of three pentominoes at various scales to form a rectangle with the four corner cells removed.

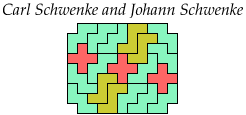
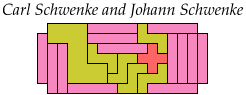
    Carl Schwenke and Johann Schwenke improved on many of my solutions.

    See also

  • Pentomino Pairs Tiling a Rectangle with Four Corner Cells Removed
  • Scaled Pentomino Pairs Tiling a Rectangle with Four Corner Cells Removed

    • Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table of Results

    This table shows the smallest total number of copies of three scaled pentominoes known to be able to tile a rectangle with four of its corner cells removed, using at least one copy of each pentomino.

    F I L7 F I N7 F I P4 F I T10 F I U7 F I V8 F I W7 F I X16 F I Y9 F I Z16
    F L N7 F L P4 F L T9 F L U7 F L V9 F L W8 F L X9 F L Y4 F L Z9 F N P4
    F N T7 F N U9 F N V9 F N W8 F N X9 F N Y4 F N Z4 F P T4 F P U7 F P V4
    F P W4 F P X9 F P Y4 F P Z7 F T U7 F T V12 F T W7 F T X33 F T Y12 F T Z9
    F U V12 F U W8 F U X7 F U Y7 F U Z7 F V W10 F V X28 F V Y9 F V Z13 F W X9
    F W Y7 F W Z7 F X Y9 F X Z? F Y Z9 I L N8 I L P5 I L T9 I L U6 I L V8
    I L W8 I L X9 I L Y7 I L Z9 I N P5 I N T8 I N U8 I N V8 I N W8 I N X4
    I N Y5 I N Z9 I P T7 I P U6 I P V5 I P W5 I P X4 I P Y6 I P Z7 I T U8
    I T V10 I T W8 I T X12 I T Y8 I T Z13 I U V6 I U W10 I U X5 I U Y8 I U Z9
    I V W9 I V X12 I V Y9 I V Z7 I W X16 I W Y9 I W Z9 I X Y4 I X Z20 I Y Z9
    L N P5 L N T9 L N U8 L N V9 L N W8 L N X10 L N Y6 L N Z8 L P T7 L P U7
    L P V7 L P W4 L P X7 L P Y5 L P Z6 L T U10 L T V10 L T W9 L T X13 L T Y7
    L T Z10 L U V8 L U W8 L U X9 L U Y8 L U Z8 L V W9 L V X10 L V Y8 L V Z10
    L W X9 L W Y8 L W Z9 L X Y9 L X Z17 L Y Z7 N P T7 N P U7 N P V4 N P W5
    N P X9 N P Y4 N P Z4 N T U8 N T V10 N T W9 N T X9 N T Y9 N T Z10 N U V10
    N U W8 N U X9 N U Y8 N U Z8 N V W9 N V X12 N V Y7 N V Z8 N W X9 N W Y8
    N W Z9 N X Y7 N X Z9 N Y Z7 P T U8 P T V7 P T W7 P T X9 P T Y7 P T Z8
    P U V7 P U W4 P U X7 P U Y4 P U Z8 P V W7 P V X9 P V Y4 P V Z7 P W X8
    P W Y4 P W Z8 P X Y7 P X Z9 P Y Z7 T U V12 T U W10 T U X12 T U Y9 T U Z14
    T V W12 T V X69 T V Y10 T V Z13 T W X16 T W Y10 T W Z16 T X Y12 T X Z? T Y Z16
    U V W8 U V X12 U V Y10 U V Z12 U W X8 U W Y8 U W Z16 U X Y7 U X Z28 U Y Z10
    V W X10 V W Y8 V W Z12 V X Y9 V X Z22 V Y Z9 W X Y12 W X Z19 W Y Z8 X Y Z12

    Solutions

    So far as I know, these solutions use as few tiles as possible. They are not necessarily uniquely minimal.

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    16 Tiles

    17 Tiles

    19 Tiles

    20 Tiles

    22 Tiles

    28 Tiles

    33 Tiles

    69 Tiles

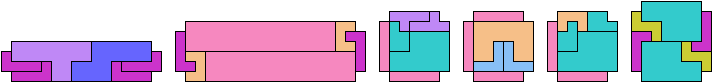
    Last revised 2024-02-27.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]