Scaled Three-Pentomino L Shapes

  • Introduction
  • Nomenclature
  • Table
  • Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

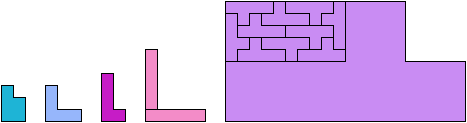
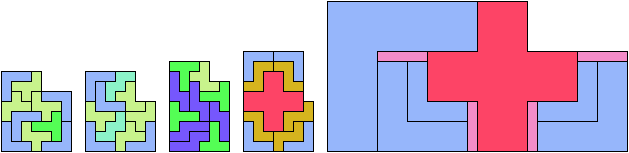
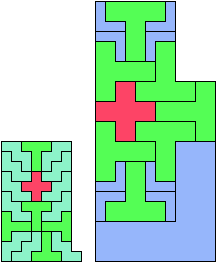
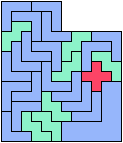
    Only five scaled pentominoes can tile L-shaped polyominoes:

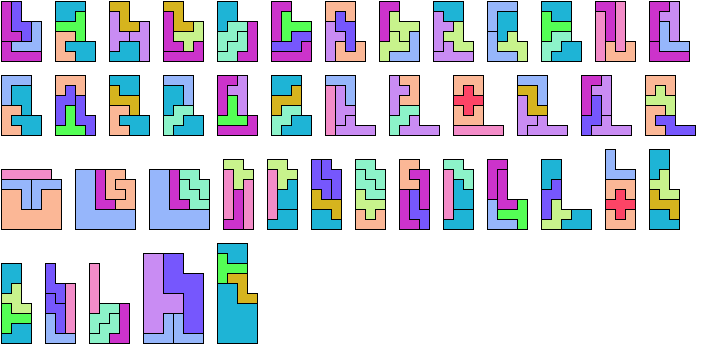
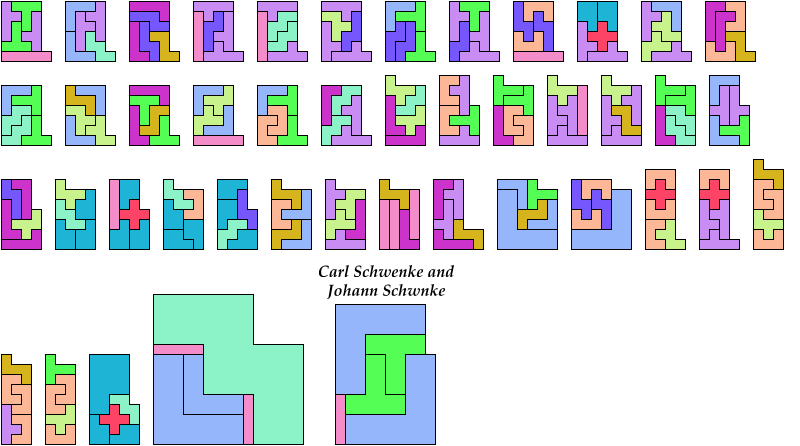
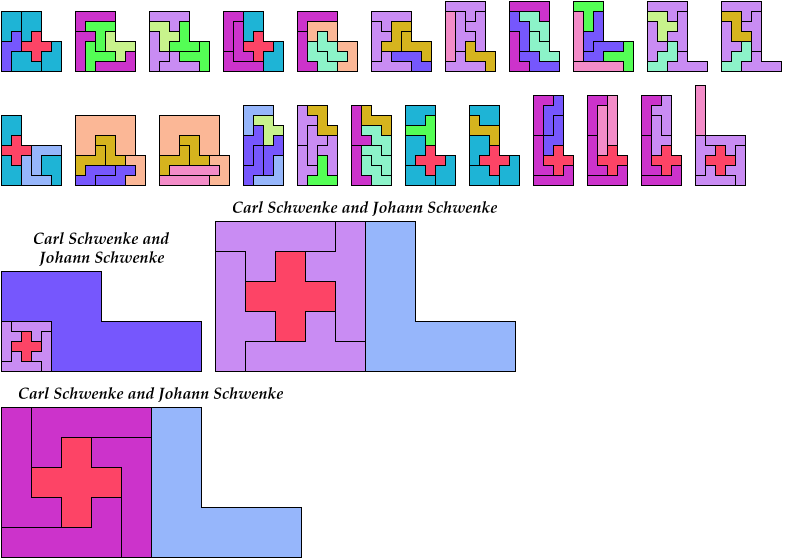
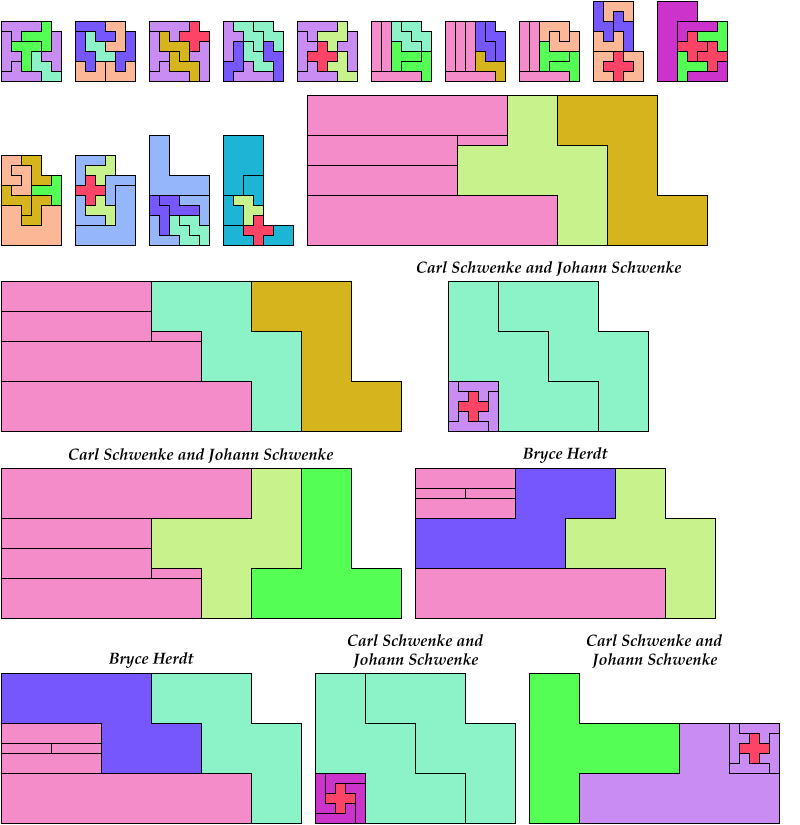
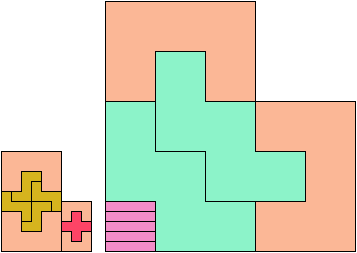
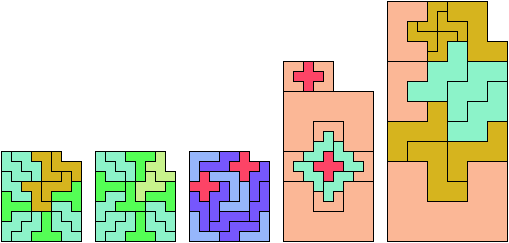
    Here I show which sets of three pentominoes can tile an L-shaped polyomino, using the pentominoes at various sizes. If you find a solution with fewer tiles than one of mine, please write!

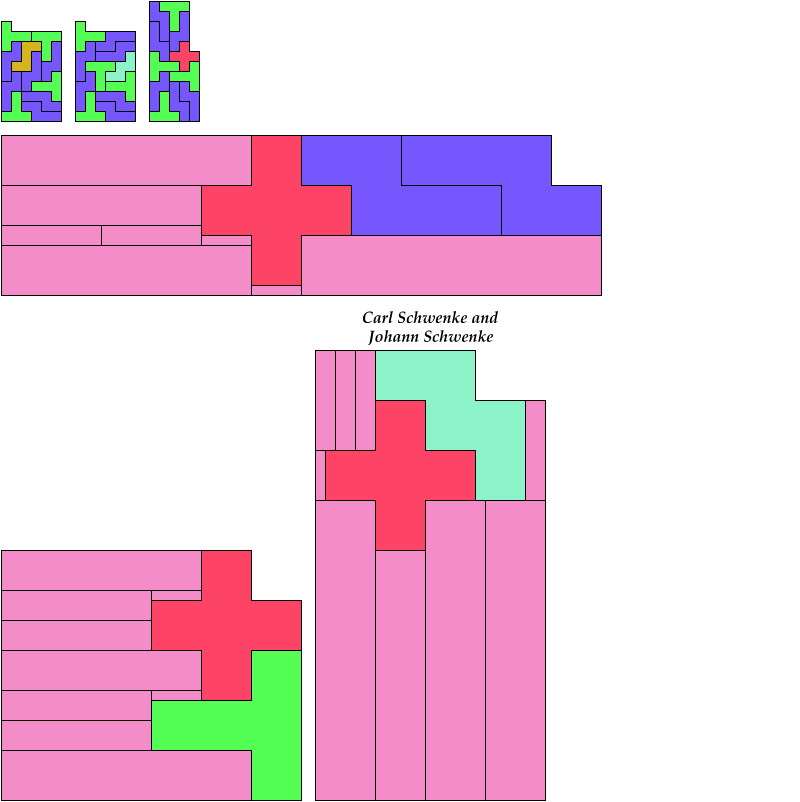
    Bryce Herdt contributed improvements. So did Carl Schwenke and Johann Schwenke.

    See also L Shapes from Three Pentominoes and Scaled Two-Pentomino L Shapes.

    Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table

    This table shows the fewest scaled pentominoes known to be able to tile some L-shaped polyomino, using at least one of each pentomino. The L-shaped polyominoes are not necessarily the smallest that can be tiled, only the smallest that can be tiled with the fewest tiles.

    FIL 4FNV 6FUZ 5INU 5IUY 3LPV 3LWZ 6NVW 8PVX 6TXZ —
    FIN 7FNW —FVW 10INV 4IUZ 7LPW 4LXY 6NVX 14PVY 3TYZ 6
    FIP 4FNX —FVX 7INW 7IVW 5LPX 6LXZ 8NVY 5PVZ 3UVW 13
    FIT 7FNY 5FVY 5INX 11IVX 10LPY 3LYZ 5NVZ 3PWX 6UVX 4
    FIU 3FNZ —FVZ 5INY 5IVY 4LPZ 3NPT 3NWX —PWY 3UVY 3
    FIV 5FPT 4FWX —INZ 7IVZ 3LTU 5NPU 3NWY 7PWZ 4UVZ 5
    FIW 8FPU 3FWY 6IPT 3IWX 11LTV 4NPV 3NWZ —PXY 5UWX 14
    FIX 12FPV 4FWZ —IPU 3IWY 5LTW 5NPW 5NXY 6PXZ 6UWY 4
    FIY 5FPW 5FXY 7IPV 3IWZ 7LTX 8NPX 6NXZ —PYZ 4UWZ 14
    FIZ 7FPX 8FXZ —IPW 4IXY 6LTY 4NPY 3NYZ 6TUV 5UXY 5
    FLN 5FPY 4FYZ 5IPX 5IXZ 12LTZ 5NPZ 4PTU 4TUW 15UXZ 11
    FLP 3FPZ 4ILN 3IPY 3IYZ 6LUV 5NTU 4PTV 3TUX 12UYZ 5
    FLT 6FTU 5ILP 3IPZ 3LNP 3LUW 6NTV 5PTW 4TUY 5VWX 27
    FLU 3FTV 10ILT 3ITU 7LNT 4LUX 3NTW 11PTX 6TUZ 7VWY 5
    FLV 4FTW 14ILU 4ITV 5LNU 4LUY 3NTX 11PTY 3TVW 5VWZ 8
    FLW 5FTX —ILV 3ITW 7LNV 4LUZ 5NTY 5PTZ 5TVX 17VXY 6
    FLX 8FTY 6ILW 4ITX 11LNW 6LVW 5NTZ 11PUV 4TVY 5VXZ 10
    FLY 5FTZ —ILX 6ITY 5LNX 6LVX 6NUV 6PUW 5TVZ 6VYZ 4
    FLZ 4FUV 3ILY 3ITZ 8LNY 4LVY 4NUW 7PUX 3TWX 17WXY 7
    FNP 4FUW 4ILZ 5IUV 7LNZ 5LVZ 3NUX 7PUY 3TWY 7WXZ —
    FNT 10FUX 5INP 3IUW 9LPT 3LWX 7NUY 4PUZ 4TWZ 14WYZ 6
    FNU 4FUY 3INT 6IUX 4LPU 3LWY 5NUZ 8PVW 4TXY 7XYZ 7

    Solutions

    So far as I know, these solutions have the fewest possible tiles. They are not necessarily uniquely minimal.

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    11 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    15 Tiles

    17 Tiles

    27 Tiles

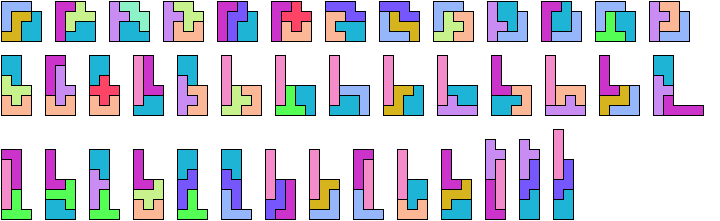
    Last revised 2024-03-26.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]